题目描述
あなたはカエル型のロボットを開発しています。 あなたはこのロボットに競走をさせることにしました。
まず、あなたは数直線上に N 体のロボットを置きました。 ロボットには 1 から N までの番号が振られています。 今、i 番目のロボットは座標 xi にいます。 ただし、xi はすべて整数であり、0 < x1 < x2 < ... < xN が成り立ちます。
あなたは次の操作を繰り返し行います。
- 数直線上のロボットを一体選ぶ。 選んだロボットの座標を x とする。 座標 x − 1, x − 2 のうち他のロボットがいない座標を着地点に選ぶ。 選んだロボットを着地点へジャンプさせる。
あるロボットの座標が 0 以下になった場合、そのロボットはゴールしたと見なされ、即座に数直線から取り除かれます。 すべてのロボットがゴールするまで、あなたは操作を行い続けます。
あなたが操作を行う方法によって、N 体のロボットがゴールする順番は何通りかありえます。 N 体のロボットがゴールする順番は何通りありうるでしょうか? 109+7 で割った余りを求めてください。
输入格式
入力は以下の形式で標準入力から与えられる。
N x1 x2 ... xN
输出格式
N 体のロボットがゴールする順番は何通りありうるか? 109+7 で割った余りを出力せよ。
3
1 2 3
4
3
2 3 4
6
8
1 2 3 5 7 11 13 17
10080
13
4 6 8 9 10 12 14 15 16 18 20 21 22
311014372
提示
制約
- 2 < = N < = 105
- xi は整数である。
- 0 < x1 < x2 < ... < xN < = 109
部分点
- 500 点分のテストケースでは、N < = 8 が成り立つ。
Sample Explanation 1
3 体のロボットがゴールする順番は、次の 4 通りありえます。 - (ロボット 1 → ロボット 2 → ロボット 3) - (ロボット 1 → ロボット 3 → ロボット 2) - (ロボット 2 → ロボット 1 → ロボット 3) - (ロボット 2 → ロボット 3 → ロボット 1)
Sample Explanation 2
3 体のロボットがゴールする順番は、次の 6 通りありえます。 - (ロボット 1 → ロボット 2 → ロボット 3) - (ロボット 1 → ロボット 3 → ロボット 2) - (ロボット 2 → ロボット 1 → ロボット 3) - (ロボット 2 → ロボット 3 → ロボット 1) - (ロボット 3 → ロボット 1 → ロボット 2) - (ロボット 3 → ロボット 2 → ロボット 1) 例えば、次図のように操作を行うと、(ロボット 3 → ロボット 2 → ロボット 1) の順にゴールします。 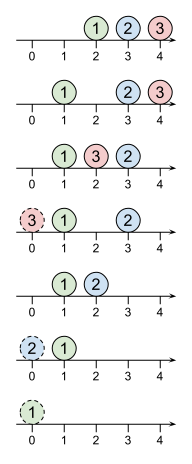
Sample Explanation 4
答えを 109+7 で割った余りを出力してください。 なお、このケースは部分点のテストケースには含まれません。
