atcoder#MUJINPC2017A. Robot Racing
Robot Racing
Score : points
Problem Statement
You are developing frog-shaped robots, and decided to race them against each other.
First, you placed robots onto a number line. These robots are numbered through . The current coordinate of robot is . Here, all are integers, and .
You will repeatedly perform the following operation:
- Select a robot on the number line. Let the coordinate of the robot be . Select the destination coordinate, either or , that is not occupied by another robot. The robot now jumps to the selected coordinate.
When the coordinate of a robot becomes or less, the robot is considered finished and will be removed from the number line immediately. You will repeat the operation until all the robots finish the race.
Depending on your choice in the operation, the robots can finish the race in different orders. In how many different orders can the robots finish the race? Find the answer modulo .
Constraints
- is an integer.
Partial Score
- In a test set worth points, .
Input
The input is given from Standard Input in the following format:
Output
Print the number of the different orders in which the robots can finish the race, modulo .
3
1 2 3
4
There are four different orders in which the three robots can finish the race:
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
3
2 3 4
6
There are six different orders in which the three robots can finish the race:
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
- Robot Robot Robot
For example, the order Robot Robot Robot can be achieved as shown in the figure below:
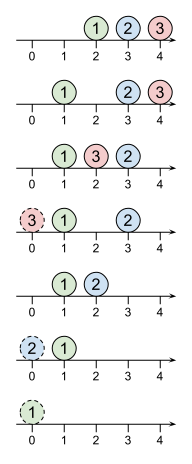
8
1 2 3 5 7 11 13 17
10080
13
4 6 8 9 10 12 14 15 16 18 20 21 22
311014372
Remember to print the answer modulo . This case is not included in the test set for the partial score.
