100 atcoder#AGC001B. [AGC001B] Mysterious Light
[AGC001B] Mysterious Light
Score : points
Problem Statement
Snuke is conducting an optical experiment using mirrors and his new invention, the rifle of Mysterious Light.
Three mirrors of length are set so that they form an equilateral triangle. Let the vertices of the triangle be and .
Inside the triangle, the rifle is placed at the point on segment such that . (The size of the rifle is negligible.) Now, the rifle is about to fire a ray of Mysterious Light in the direction of .
The ray of Mysterious Light will travel in a straight line, and will be reflected by mirrors, in the same ways as "ordinary" light. There is one major difference, though: it will be also reflected by its own trajectory as if it is a mirror! When the ray comes back to the rifle, the ray will be absorbed.
The following image shows the ray's trajectory where and .
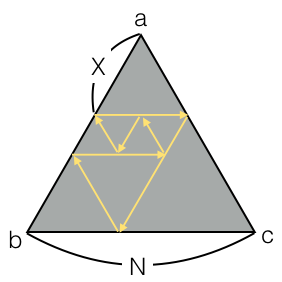
It can be shown that the ray eventually comes back to the rifle and is absorbed, regardless of the values of and . Find the total length of the ray's trajectory.
Constraints
- and are integers.
Partial Points
- points will be awarded for passing the test set satisfying .
- Another points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
Output
Print the total length of the ray's trajectory.
5 2
12
Refer to the image in the Problem Statement section. The total length of the trajectory is .
