Description

Given $n$ circles $c_1,$ $c_2,$ $\ldots,$ $c_n$ on a flat Cartesian plane. We attempt to do the following:

1. Find the circle $c_i$ with the largest radius. If there are multiple candidates all having the same (largest) radius, choose the one with the smallest index. (i.e. minimize $i$).
2. Remove $c_i$ and all the circles intersecting with $c_i$. Two circles intersect if there exists a point included by both circles. A point is included by a circle if it is located in the circle or on the border of the circle.
3. Repeat 1 and 2 until there is no circle left.

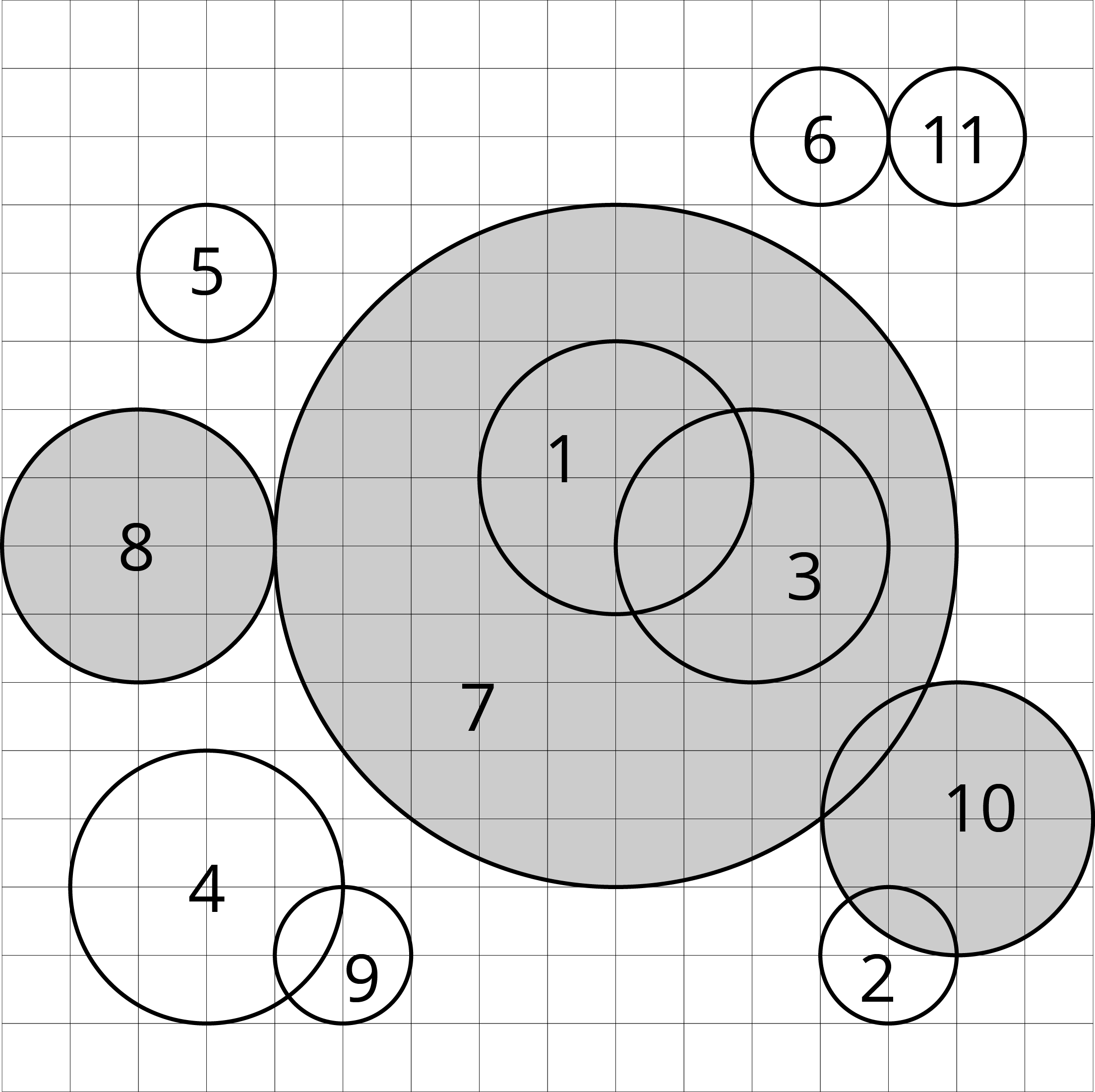
We say $c_i$ is eliminated by $c_j$ if $c_j$ is the chosen circle in the iteration where $c_i$ is removed. For each circle, find out the circle by which it is eliminated.

Input

The first line contains an integer $n$, denoting the number of circles $(1 ≤ n ≤ 3\times 10^5)$.

Each of the next $n$ lines contains three integers $x_i,$ $y_i,$ $r_i,$ representing the $x$-coordinate, the $y$-coordinate, and the radius of the circle $c_i$ $(−10^9 ≤ x_i,$ $y_i ≤ 10^9,$ $1 ≤ r_i ≤ 10^9).$

Output

Output $n$ integers $a_1,$ $a_2,$ $\ldots,$ $a_n$ in the first line, where $a_i$ means that $c_i$ is eliminated by $c_{a_i}.$

11
9 9 2
13 2 1
11 8 2
3 3 2
3 12 1
12 14 1
9 8 5
2 8 2
5 2 1
14 4 2
14 14 1

7 2 7 4 5 6 7 7 4 7 6

Limits And Hints

Subtask 1 (7 points): $n \le 5000$

Subtask 2 (12 points): $n \le 3 \cdot 10^5,$ $y_i=0$ for all circles.

Subtask 3 (15 points): $n \le 3 \cdot 10^5$, every circle intersects with at most 1 other circle.

Subtask 4 (23 points): $n \le 3 \cdot 10^5$, all circles have the same radius.

Subtask 5 (30 points): $n \le 10^5$

Subtask 6 (13 points): $n \le 3 \cdot 10^5$