atcoder#MUJINPC2017B. Row to Column
Row to Column
Score : points
Problem Statement
There is a square-shaped grid with vertical rows and horizontal columns. We will denote the square at the -th row from the top and the -th column from the left as .
Initially, each square is either white or black.
The initial color of the grid is given to you as characters , arranged in a square shape.
If the square is white, is .. If it is black, is #.
You are developing a robot that repaints the grid. It can repeatedly perform the following operation:
- Select two integers , (). Memorize the colors of the squares , , , as , , , , respectively. Then, repaint the squares , , , with the colors , , , , respectively.
Your objective is to turn all the squares black. Determine whether it is possible, and find the minimum necessary number of operations to achieve it if the answer is positive.
Constraints
- is either
.or#.
Partial Score
- In a test set worth points, .
Input
The input is given from Standard Input in the following format:
Output
If it is possible to turn all the squares black, print the minimum necessary number of operations to achieve the objective.
If it is impossible, print -1 instead.
2
#.
.#
3
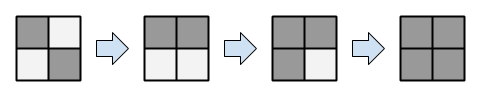
For example, perform the operation as follows:
- Select , .
- Select , .
- Select , .
The transition of the colors of the squares is shown in the figure below:
2
..
..
-1
2
##
##
0
3
.#.
###
.#.
2
3
...
.#.
...
5
