atcoder#CODEFESTIVAL2017QUALAE. Modern Painting
Modern Painting
配点 : 点
問題文
現代美術に興味を持ったりんごさんは、CODE FESTIVAL 2017 の会場に作られた 行 列の盤面と、何人かの人を使って絵を描くことにしました。
盤面の上から 行目、左から 列目のマスは つの整数の組 であらわされます。すなわち、左上のマスが で、右下のマスが です。 最初、 を満たすマス は白で塗られており、それ以外の (外周の) マスは黒で塗られています。
りんごさんは、盤面の外周のマスのうちのいくつかに、人を内向きに配置しました。 より厳密には、配置の情報は つの文字列 によってあらわされ、以下のように配置が行われます。
- 端以外の各行について、 の 文字目が
1のときマス に、右を向いた人を 人配置する。そうでないとき、何もしない。 - 端以外の各行について、 の 文字目が
1のときマス に、左を向いた人を 人配置する。そうでないとき、何もしない。 - 端以外の各列について、 の 文字目が
1のときマス に、下を向いた人を 人配置する。そうでないとき、何もしない。 - 端以外の各列について、 の 文字目が
1のときマス に、上を向いた人を 人配置する。そうでないとき、何もしない。
各人はそれぞれ、白でない色のペンキを充分な量持っています。どの相異なる 人の持っているペンキの色も、互いに異なります。
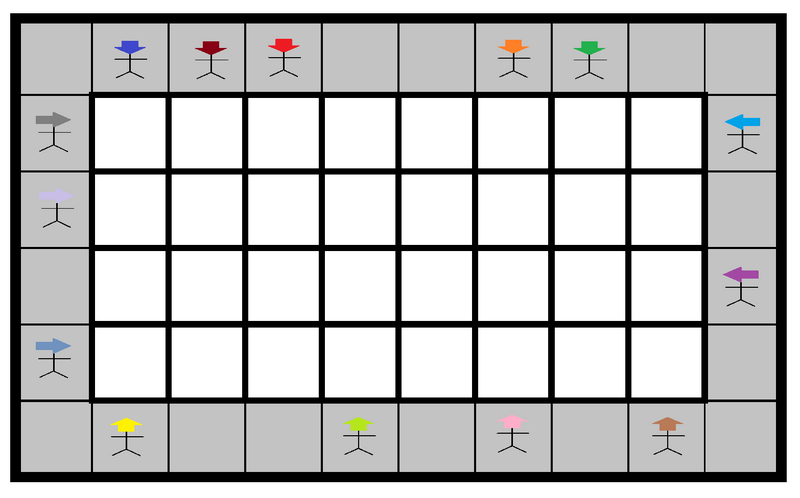
人の配置の例(便宜上、黒く塗られたマスを灰色で表しています)
りんごさんは、以下の一連の操作を、全ての人が会場から追い出されていなくなるまで繰り返します。
- まだ追い出されていない人を 人選ぶ。
- 選ばれた人は、目の前のマスが白で塗られている間、自分の向いている向きに マス分進み、進んだ先のマスを自分の持っているペンキで塗る。目の前のマスが白で塗られていない場合、動作を終了する。
- 動作を終了した人を会場から追い出す。
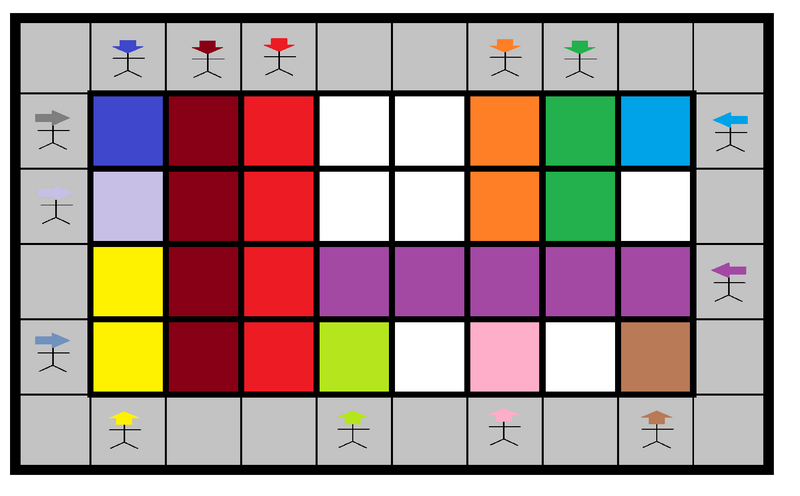
塗られ方の例
りんごさんが作ることのできる、最終的な盤面の塗られ方は何通りあるでしょうか。 で割ったあまりを求めてください。
なお、 つの盤面の塗られ方が異なるとは、あるマスが存在し、そのマスの色が異なることを指します。
制約
- は
0と1からなる
入力
入力は以下の形式で標準入力から与えられる。
出力
最終的な盤面の塗られ方の総数を で割ったあまりを出力せよ。
2 2
10
01
10
01
6
以下の 通りの塗られ方があります。
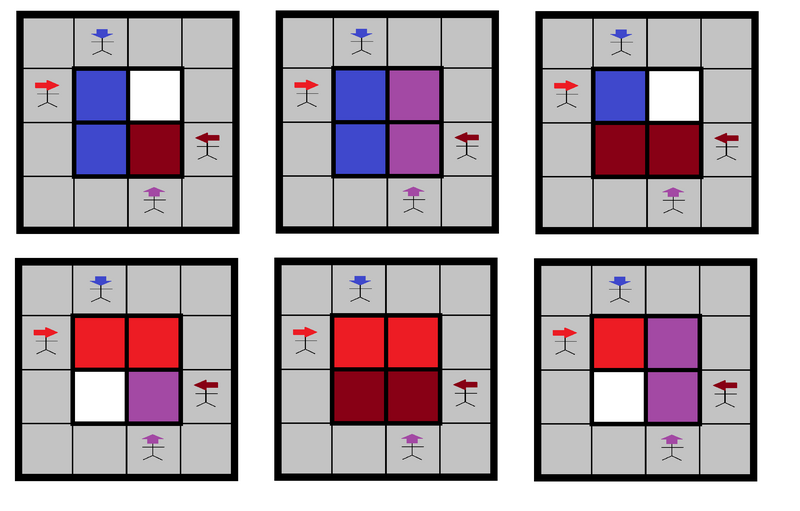
2 2
11
11
11
11
32
3 4
111
111
1111
1111
1276
17 21
11001010101011101
11001010011010111
111010101110101111100
011010110110101000111
548356548
で割ったあまりを求めるのを忘れないようにしてください。
3 4
000
101
1111
0010
21
9 13
111100001
010101011
0000000000000
1010111111101
177856
23 30
01010010101010010001110
11010100100100101010101
000101001001010010101010101101
101001000100101001010010101000
734524988
