atcoder#CODEFESTIVAL2016FINALG. Zigzag MST
Zigzag MST
题目描述
個の頂点からなるグラフがあり、頂点には の番号が付けられています。辺はまだありません。
辺を追加するクエリを 個処理します。 番目のクエリでは の つの整数が与えられるので、以下のように辺を無限本追加します。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- 番の頂点と 番の頂点をつなぐ、重み の無向辺を追加する。
- ...
ただし、頂点番号は mod で考えます。 たとえば、 番とは 番のことであり、 番とは 番のことです。
例えば、 のときは下図のように辺を追加します。(図では最初の 本のみ)
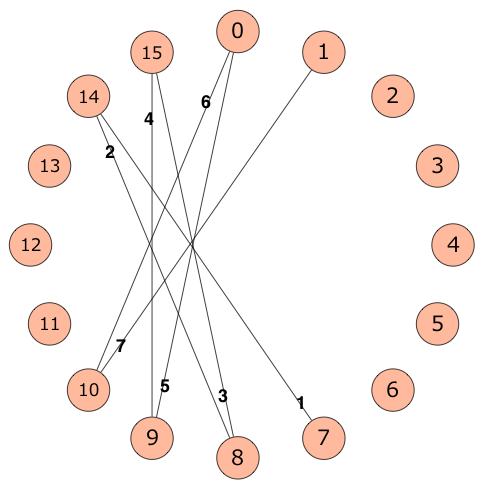
すべての辺を追加した後のグラフの最小全域木に含まれる辺の重みの和を求めて下さい。
输入格式
入力は以下の形式で標準入力から与えられる。
:
输出格式
最小全域木に含まれる辺の重みの和を出力せよ。
题目大意
对一张 n 个点的图做Q次加边操作,每次给定 Ai, Bi, Ci,然后按顺序连边(Ai,Bi,Ci),(Bi,Ai+1,Ci+1),(Ai+1,Bi+1,Ci+2)等等,求给定图的最小生成树。(Ai,Bi,Ci等点编号均为对n取模的意义下) 给定 初始的n,q,Ai,Bi,Ci; (2≦N≦200,000)(1≦Q≦200,000) (0≦Ai,Bi≦N−1)(1≦Ci≦10^9)
7 1
5 2 1
21
2 1
0 0 1000000000
1000000001
5 3
0 1 10
0 2 10
0 4 10
42
提示
制約
Sample Explanation 1
最小全域木は下図のようになります。 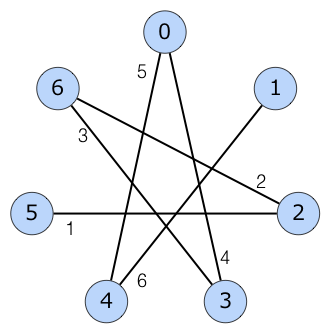 多重辺が存在しうることに注意して下さい。
Sample Explanation 2
自己ループが存在しうることに注意して下さい。
