Score : $1000$ points

Problem Statement

There are $N$ towns in Takahashi Kingdom. They are conveniently numbered $1$ through $N$.

Takahashi the king is planning to go on a tour of inspection for $M$ days. He will determine a sequence of towns $c$, and visit town $c_i$ on the $i$-th day. That is, on the $i$-th day, he will travel from his current location to town $c_i$. If he is already at town $c_i$, he will stay at that town. His location just before the beginning of the tour is town $1$, the capital. The tour ends at town $c_M$, without getting back to the capital.

The problem is that there is no paved road in this kingdom. He decided to resolve this issue by paving the road himself while traveling. When he travels from town $a$ to town $b$, there will be a newly paved one-way road from town $a$ to town $b$.

Since he cares for his people, he wants the following condition to be satisfied after his tour is over: "it is possible to travel from any town to any other town by traversing roads paved by him". How many sequences of towns $c$ satisfy this condition?

Constraints

• $2 \leq N \leq 300$
• $1 \leq M \leq 300$

Input

The input is given from Standard Input in the following format:

$N$ $M$

Output

Print the number of sequences of towns satisfying the condition, modulo $1000000007 (=10^9+7)$.

3 3

2

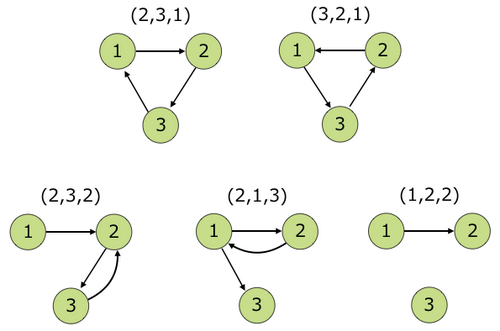
As shown below, the condition is satisfied only when $c = (2,3,1)$ or $c = (3,2,1)$. Sequences such as $c = (2,3,2)$, $c = (2,1,3)$, $c = (1,2,2)$ do not satisfy the condition.

150 300

734286322

300 150

0