配点 : $900$ 点

問題文

モグラは $1$ から $N$ の番号がついた $N$ 個の頂点と $M$ 本の辺からなる単純連結無向グラフで表されるような廃坑に住むことにしました。 $i$ 番目の辺は頂点 $a_i$ と $b_i$ をつないでおり、取り除くために $c_i$ 円かかります。

モグラはいくつかの辺を取り除いて、頂点 $1$ から頂点 $N$ へ同じ頂点を $2$ 回以上訪れないように移動する経路がただ $1$ 通りのみ存在するようにしたいです。これを達成するために必要な資金の最小値を求めなさい。

制約

• $2 \leq N \leq 15$
• $N-1 \leq M \leq N(N-1)/2$
• $1 \leq a_i, b_i \leq N$
• $1 \leq c_i \leq 10^{6}$
• 与えられるグラフに多重辺や自己ループは存在しない
• 与えられるグラフは連結

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$

$a_1$ $b_1$ $c_1$

$:$

$a_M$ $b_M$ $c_M$

出力

答えを出力せよ。

4 6
1 2 100
3 1 100
2 4 100
4 3 100
1 4 100
3 2 100

200

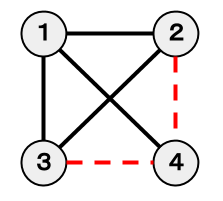
以下の図において、赤い破線で表されている辺は取り除かれた辺です。以下の図のように $2$ つの辺を取り除くことで $200$ 円で達成することが可能です。

2 1
1 2 1

0

はじめから、頂点 $1$ から頂点 $N$ へのパスが $1$ 通りしかないこともあります。

15 22
8 13 33418
14 15 55849
7 10 15207
4 6 64328
6 9 86902
15 7 46978
8 14 53526
1 2 8720
14 12 37748
8 3 61543
6 5 32425
4 11 20932
3 12 55123
8 2 45333
9 12 77796
3 9 71922
12 15 70793
2 4 25485
11 6 1436
2 7 81563
7 11 97843
3 1 40491

133677