atcoder#ARC070C. [ARC070E] NarrowRectangles
[ARC070E] NarrowRectangles
Score : points
Problem Statement
AtCoDeer the deer found rectangle lying on the table, each with height . If we consider the surface of the desk as a two-dimensional plane, the -th rectangle covers the vertical range of and the horizontal range of , as shown in the following figure:
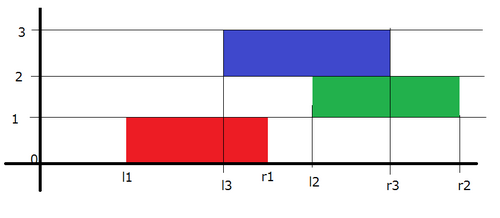
AtCoDeer will move these rectangles horizontally so that all the rectangles are connected. For each rectangle, the cost to move it horizontally by a distance of , is . Find the minimum cost to achieve connectivity. It can be proved that this value is always an integer under the constraints of the problem.
Constraints
- All input values are integers.
- $1 \leq l_i
Partial Score
- points will be awarded for passing the test set satisfying and $1 \leq l_i.
Input
The input is given from Standard Input in the following format:
:
Output
Print the minimum cost to achieve connectivity.
3
1 3
5 7
1 3
2
The second rectangle should be moved to the left by a distance of .
3
2 5
4 6
1 4
0
The rectangles are already connected, and thus no move is needed.
5
999999999 1000000000
1 2
314 315
500000 500001
999999999 1000000000
1999999680
5
123456 789012
123 456
12 345678901
123456 789012
1 23
246433
1
1 400
0
