atcoder#ARC063D. [ARC063F] すぬけ君の塗り絵 2
[ARC063F] すぬけ君の塗り絵 2
Score : points
Problem Statement
There is a rectangle in the -plane, with its lower left corner at and its upper right corner at . Each of its sides is parallel to the -axis or -axis. Initially, the whole region within the rectangle is painted white.
Snuke plotted points into the rectangle. The coordinate of the -th () point was .
Then, for each , he will paint one of the following four regions black:
- the region satisfying within the rectangle
- the region satisfying within the rectangle
- the region satisfying within the rectangle
- the region satisfying within the rectangle
Find the longest possible perimeter of the white region of a rectangular shape within the rectangle after he finishes painting.
Constraints
- ()
- ()
- , (21:32, added), and are integers.
- If , then and .
Input
The input is given from Standard Input in the following format:
Output
Print the longest possible perimeter of the white region of a rectangular shape within the rectangle after Snuke finishes painting.
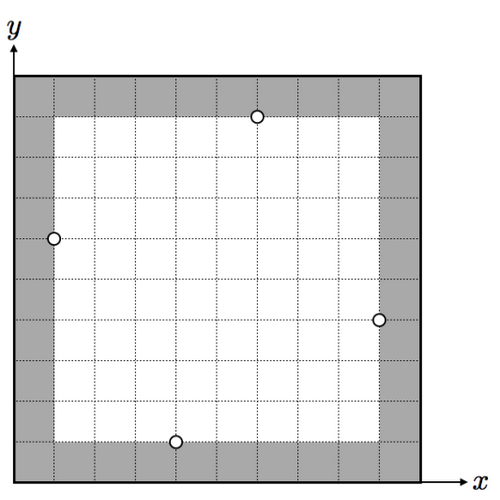
10 10 4
1 6
4 1
6 9
9 4
32
In this case, the maximum perimeter of can be obtained by painting the rectangle as follows:
5 4 5
0 0
1 1
2 2
4 3
5 4
12
100 100 8
19 33
8 10
52 18
94 2
81 36
88 95
67 83
20 71
270
100000000 100000000 1
3 4
399999994
