atcoder#AGC041E. [AGC041E] Balancing Network
[AGC041E] Balancing Network
Score : points
Problem Statement
A balancing network is an abstract device built up of wires, thought of as running from left to right, and balancers that connect pairs of wires. The wires are numbered from to from top to bottom, and the balancers are numbered from to from left to right. Balancer connects wires and ().
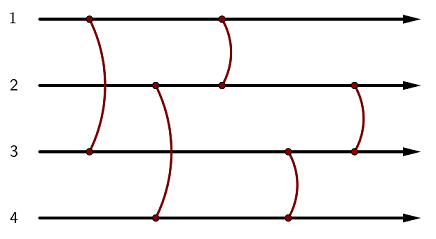
Each balancer must be in one of two states: up or down.
Consider a token that starts moving to the right along some wire at a point to the left of all balancers. During the process, the token passes through each balancer exactly once. Whenever the token encounters balancer , the following happens:
- If the token is moving along wire and balancer is in the down state, the token moves down to wire and continues moving to the right.
- If the token is moving along wire and balancer is in the up state, the token moves up to wire and continues moving to the right.
- Otherwise, the token doesn't change the wire it's moving along.
Let a state of the balancing network be a string of length , describing the states of all balancers.
The -th character is ^ if balancer is in the up state, and v if balancer is in the down state.
A state of the balancing network is called uniforming if a wire exists such that, regardless of the starting wire, the token will always end up at wire and run to infinity along it. Any other state is called non-uniforming.
You are given an integer (). Answer the following question:
- If , find any uniforming state of the network or determine that it doesn't exist.
- If , find any non-uniforming state of the network or determine that it doesn't exist.
Note that if you answer just one kind of questions correctly, you can get partial score.
Constraints
- All input values are integers.
Partial Score
- points will be awarded for passing the testset satisfying .
- points will be awarded for passing the testset satisfying .
Input
Input is given from Standard Input in the following format:
Output
Print any uniforming state of the given network if , or any non-uniforming state if . If the required state doesn't exist, output -1.
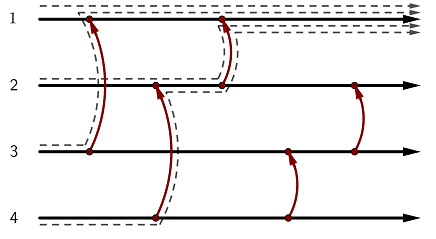
4 5 1
1 3
2 4
1 2
3 4
2 3
^^^^^
This state is uniforming: regardless of the starting wire, the token ends up at wire .
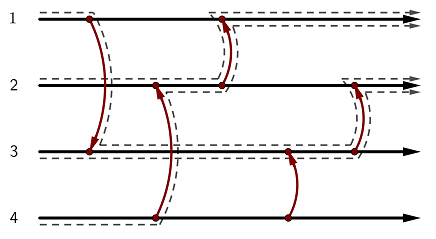
4 5 2
1 3
2 4
1 2
3 4
2 3
v^^^^
This state is non-uniforming: depending on the starting wire, the token might end up at wire or wire .
3 1 1
1 2
-1
A uniforming state doesn't exist.
2 1 2
1 2
-1
A non-uniforming state doesn't exist.
