atcoder#AGC011F. [AGC011F] Train Service Planning
[AGC011F] Train Service Planning
Score : points
Problem Statement
There is a railroad in Takahashi Kingdom. The railroad consists of sections, numbered , , ..., , and stations, numbered , , ..., . Section directly connects the stations and . A train takes exactly minutes to run through section , regardless of direction. Each of the sections is either single-tracked over the whole length, or double-tracked over the whole length. If , section is single-tracked; if , section is double-tracked. Two trains running in opposite directions can cross each other on a double-tracked section, but not on a single-tracked section. Trains can also cross each other at a station.
Snuke is creating the timetable for this railroad. In this timetable, the trains on the railroad run every minutes, as shown in the following figure. Here, bold lines represent the positions of trains running on the railroad. (See Sample 1 for clarification.)
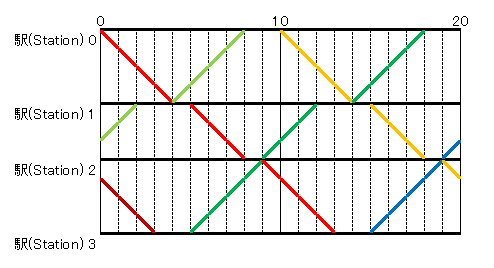
When creating such a timetable, find the minimum sum of the amount of time required for a train to depart station and reach station , and the amount of time required for a train to depart station and reach station . It can be proved that, if there exists a timetable satisfying the conditions in this problem, this minimum sum is always an integer.
Formally, the times at which trains arrive and depart must satisfy the following:
- Each train either departs station and is bound for station , or departs station and is bound for station .
- Each train takes exactly minutes to run through section . For example, if a train bound for station departs station at time , the train arrives at station exactly at time .
- Assume that a train bound for station arrives at a station at time , and departs the station at time . Then, the next train bound for station arrives at the station at time , and departs the station at time . Additionally, the previous train bound for station arrives at the station at time , and departs the station at time . This must also be true for trains bound for station .
- Trains running in opposite directions must not be running on the same single-tracked section (except the stations at both ends) at the same time.
Constraints
- is an integer.
- is either or .
Partial Score
- In the test set worth points, all the sections are single-tracked. That is, .
- In the test set worth another points, .
Input
The input is given from Standard Input in the following format:
:
Output
Print an integer representing the minimum sum of the amount of time required for a train to depart station and reach station , and the amount of time required for a train to depart station and reach station . If it is impossible to create a timetable satisfying the conditions, print instead.
3 10
4 1
3 1
4 1
26
For example, the sum of the amount of time in question will be minutes in the following timetable:

In this timetable, the train represented by the red line departs station at time , arrives at station at time , departs station at time , arrives at station at time , and so on.
1 10
10 1
-1
6 4
1 1
1 1
1 1
1 1
1 1
1 1
12
20 987654321
129662684 2
162021979 1
458437539 1
319670097 2
202863355 1
112218745 1
348732033 1
323036578 1
382398703 1
55854389 1
283445191 1
151300613 1
693338042 2
191178308 2
386707193 1
204580036 1
335134457 1
122253639 1
824646518 2
902554792 2
14829091348
