uoj#P567. 【IOI2020】Biscuits
【IOI2020】Biscuits
由于某些原因本题仅支持 C++, C++11 语言的提交。
Khong 阿姨在组织一场有 $x$ 位选手参加的竞赛,她打算给每位选手一袋饼干。总共有 $k$ 种不同类型的饼干,编号为从 $0$ 到 $k - 1$。类型为 $i$($0 \le i \le k - 1$)的每块饼干都有一个口味值 $2^i$。在 Khong 阿姨的食品储藏室里,有 $a_i$(有可能为 $0$)块类型为 $i$ 的饼干。
对每种类型的饼干,Khong 阿姨在每个袋子都会装上 $0$ 或者多块。所有袋子里面类型为 $i$ 的饼干的总块数不能超过 $a_i$。一个袋子里面所有饼干的口味值的总和,被称为这袋饼干的总口味值。
请帮 Khong 阿姨算一下,究竟存在多少不同的 $y$ 值,使得她可以装出 $x$ 袋饼干,而且每袋饼干的总口味值都等于 $y$。
实现细节
你必须引用 biscuits.h 头文件。
你需要实现以下函数:
long long count_tastiness(long long x, std::vector<long long> a)- $x$:需要装的饼干袋的数量。
- $a$:长度为 $k$ 的数组。对 $0 \le i \le k - 1$,$a_i$ 表示在食物储藏室里类型为 $i$ 的饼干数量。
- 此函数应当返回不同 $y$ 值的数目,使得阿姨可以装出 $x$ 袋饼干,且每袋饼干的总口味值都为 $y$。
- 此函数会被调用 $q$ 次(对于允许的 $q$ 值,详见约束条件和子任务部分)。每次调用应当被看成是独立的场景。
输入格式
评测程序示例将读取如下格式的输入数据。第一行包含一个整数 $q$。接下来是 $q$ 对这样的两行:它们按照下面的格式来描述一个单独的场景:
- 第一行:$k\ x$
- 第二行:$a_0\ a_1\ \ldots\ a_{k - 1}$
输出格式
评测程序示例的输出结果的格式如下:
- 第 $i$ 行($1 \le i \le q$):
count_tastiness对于输入数据中第 $i$ 个场景的返回值。
2
3 3
5 2 1
3 2
2 1 2
5
6
对于第一组数据: 考虑以下调用:
count_tastiness(3, [5, 2, 1])这意味着阿姨打算装 $3$ 袋饼干,而在食物储藏室里总共有 $3$ 种类型的饼干: - $5$ 块类型为 $0$ 的饼干,每块的口味值为 $1$, - $2$ 块类型为 $1$ 的饼干,每块的口味值为 $2$, - $1$ 块类型为 $2$ 的饼干,其口味值为 $4$。
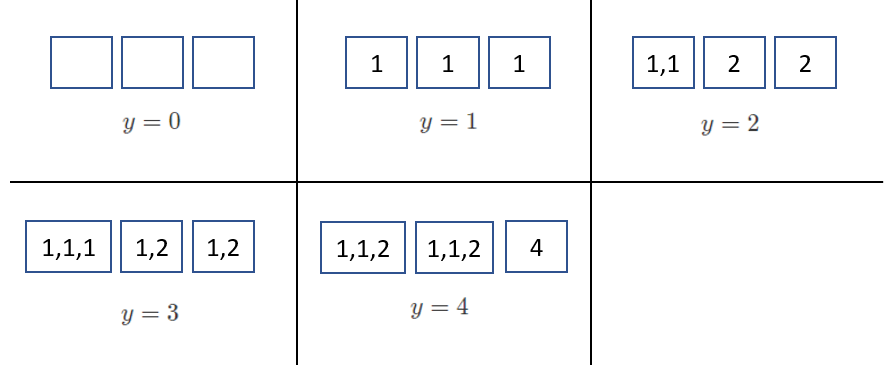
$y$ 能够取的值为 $[0,1,2,3,4]$。举例来说,为了装出总口味值均为 $3$ 的 $3$ 袋饼干,阿姨可以这样装:
- 一袋饼干里有 $3$ 块类型为 $0$ 的饼干,以及
- 两袋饼干,其中各有一块类型为 $0$ 的饼干和一块类型为 $1$ 的饼干。
由于总共有 $5$ 个可能的 $y$ 值,函数应当返回 $5$。
对于第二组数据:
考虑如下调用:
count_tastiness(2, [2, 1, 2])这意味着阿姨打算装 $2$ 袋饼干,而在食物储藏室里总共有 $3$ 种类型的饼干: - $2$ 块类型为 $0$ 的饼干,每块的口味值为 $1$, - $1$ 块类型为 $1$ 的饼干,其口味值为 $2$, - $2$ 块类型为 $2$ 的饼干,每块的口味值为 $4$。
$y$ 能够取的值为 $[0,1,2,4,5,6]$,由于总共有 $6$ 个可能的 $y$ 值,函数应当返回 $6$。
限制与约定
对于全部数据,满足:
- $1\le k\le 60$
- $1\le q\le 1000$
- $1\le x\le 10^{18}$
- $0\le a_i\le 10^{18}$(对于所有的 $0\le i\le k-1$)
- 对于
count_tastiness的每次调用,食物储藏室里所有饼干的口味值总和都不会超过 $10^{18}$。
详细子任务分值与附加限制如下表:
| 子任务 | 附加限制 | 分值 |
|---|---|---|
| $1$ | $q\le 10$,且对于 count_tastiness 的每次调用,食物储藏室里所有饼干的口味值总和都不会超过 $100\ 000$。 |
$9$ |
| $2$ | $x=1,q\le 10$ | $12$ |
| $3$ | $x\le 10\ 000,q\le 10$ | $21$ |
| $4$ | 对于 count_tastiness 的每次调用,正确的返回结果都不会超过 $200\ 000$。 |
$35$ |
| $5$ | 没有附加限制条件。 | $23$ |
时间限制:$1 \texttt{s}$
空间限制:$1024 \texttt{MB}$
