uoj#P375. 【ZJOI2018】迷宫
【ZJOI2018】迷宫
九条可怜是一个贪玩的女孩子。
暑假快要到了,可怜打算在她家的私人海滩旁边建一座城堡,这样就可以在放暑假的时候邀请她的朋友们来玩了。同时,可怜打算在城堡的地下修建一座迷宫,因为探险总是一件充满乐趣的事情。
经过简单的设计,可怜打算修建一座这样的迷宫:
- 迷宫可以被抽象成 $n$ 个点,$nm$ 条边的有向图。$1$ 号点是唯一的入口也是唯一的出口。
- 每一个点恰好有 $m$ 条出边,且这些出边被依次标号为 $[0, m)$ 的正整数。
- 迷宫允许自环和重边。
同时,一座优秀的迷宫应该有一定的解谜因素。因此可怜希望每一条从 $1$ 号点出发并回到 $1$ 号点的回路都有着一定的规律。
可怜发现,如果把一条从 $1$ 出发的路径经过的所有边的编号都记录下来,那么能得到一个 (可能有前导 $0$)的 $m$ 进制数;同时对于每一个(可能有前导 $0$)的 $m$ 进制数,都能对应回一条从 $1$ 出发的路径。
于是可怜选定了一个整数 $K$,她希望这个迷宫满足一条从 $1$ 出发的路径能回到 $1$ 当且仅当这条路径对应的数是 $K$ 的倍数。
现在可怜已经选定了 $m$ 和 $K$,但是她发现并不是对所有的 $n$,都存在满足上述所有条件的迷宫设计方案。建造迷宫是一件费时费力的事情,于是可怜想要找到一个最小的满足条件的 $n$。 然而可怜对复杂的计算并不感兴趣,因此她想让你来帮她计算一下这个数值。
输入格式
第一行输入一个整数 $T$ 表示数据组数。
接下来 $T$ 行每行两个十进制正整数 $m, K$ 表示可怜选定的整数。
输出格式
对于每组数据,输出一行一个整数表示能够满足所有条件的最小的 $n$。如果不存在这样的 $n$,输出 $−1$。
3
2 3
2 4
6 8
3
3
5
第一组数据(左)和第二组数据(右)的一种设计方案如下图所示。其中紫色边表示 $0$ 号边,蓝色边表示 $1$ 号边。
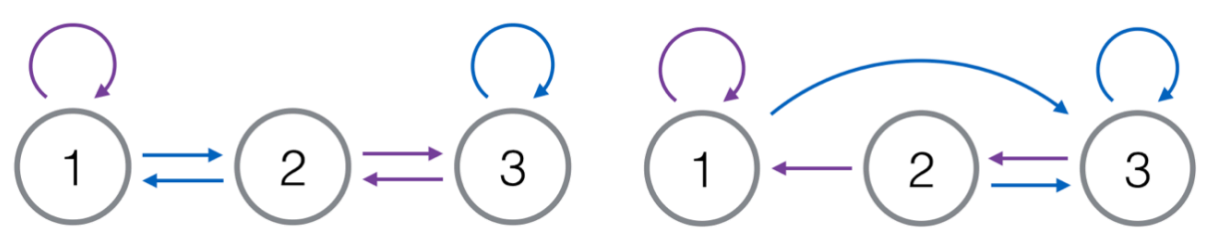
样例二
见样例数据下载
数据范围与约定
$m\ge 2$
| 测试点 | $m$ | $K$ | $t$ | 其他约定 |
|---|---|---|---|---|
| 1 | $\le 6$ | $\le 10$ | $\le 100$ | 无 |
| 2 | $\le 100$ | $\le 100$ | $\le 100$ | 无 |
| 3 | $\le 100$ | $\le 100$ | $\le 100$ | 无 |
| 4 | $\le 10^5$ | $\le 10^5$ | $\le 100$ | 无 |
| 5 | $\le 10^5$ | $\le 10^5$ | $\le 100$ | 无 |
| 6 | $\le 10^9$ | $\le 10^9$ | $\le 1000$ | $m$为质数 |
| 7 | $\le 10^9$ | $\le 10^9$ | $\le 1000$ | 无 |
| 8 | $\le 10^9$ | $\le 10^9$ | $\le 1000$ | 无 |
| 9 | $\le 10^{18}$ | $\le 10^{18}$ | $\le 3\times 10^5$ | 无 |
| 10 | $\le 10^{18}$ | $\le 10^{18}$ | $\le 3\times 10^5$ | 无 |
时间限制:$1\texttt{s}$
空间限制:$512\texttt{MB}$
