uoj#P260. 【NOIP2016】玩具谜题
【NOIP2016】玩具谜题
小南有一套可爱的玩具小人,它们各有不同的职业。
有一天,这些玩具小人把小南的眼镜藏了起来。小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
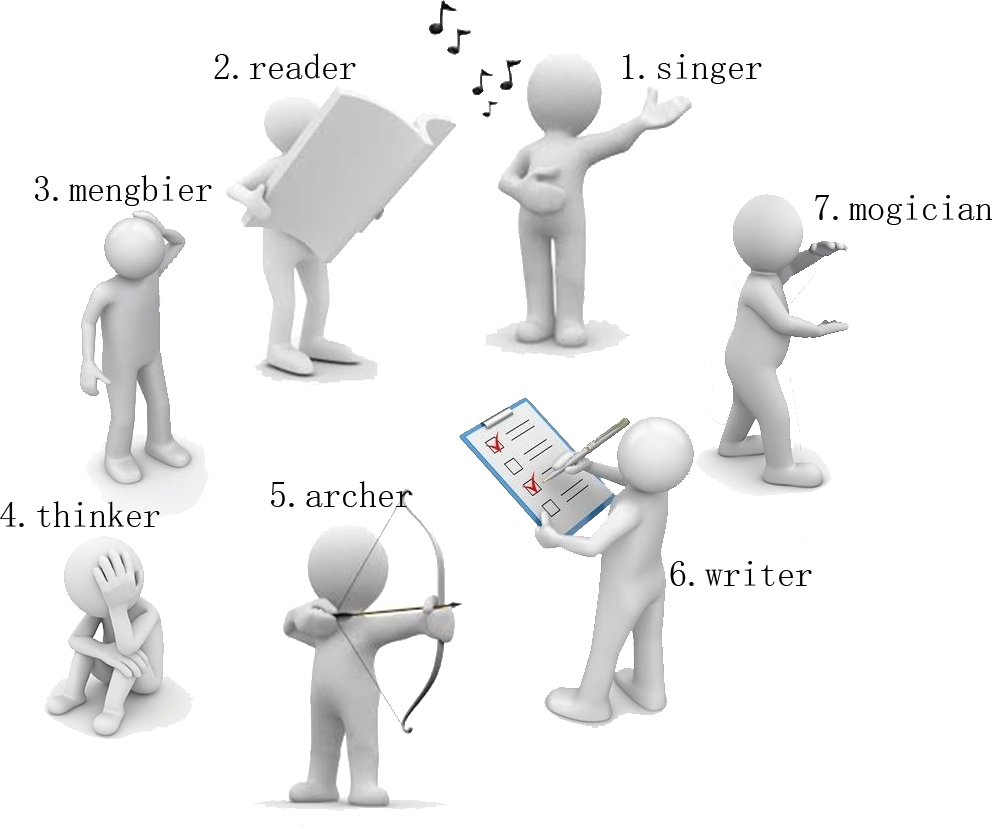
这时 singer 告诉小南一个谜题:“眼镜藏在我左数第 $3$ 个玩具小人的右数第 $1$ 个玩具小人的左数第 $2$ 个玩具小人那里。”
小南发现,这个谜题中玩具小人的朝向非常关键,因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人,它的左边是顺时针方向,右边是逆时针方向;而面向圈外的玩具小人,它的左边是逆时针方向,右边是顺时针方向。
小南一边艰难地辨认着玩具小人,一边数着:
“singer 朝内,左数第 $3$ 个是 archer。
“archer 朝外,右数第 $1$ 个是 thinker。
“thinker 朝外,左数第 $2$ 个是 writer。
“所以眼镜藏在 writer 这里!”
虽然成功找回了眼镜,但小南并没有放心。如果下次有更多的玩具小人藏他的眼镜,或是谜题的长度更长,他可能就无法找到眼镜了。 所以小南希望你写程序帮他解决类似的谜题。这样的谜题具体可以描述为:
有 $n$ 个玩具小人围成一圈,已知它们的职业和朝向。现在第 $1$ 个玩具小人告诉小南一个包含 $m$ 条指令的谜题,其中第 $i$ 条指令形如“左数/右数第 $s_i$ 个玩具小人”。
你需要输出依次数完这些指令后,到达的玩具小人的职业。
输入格式
从标准输入读入数据。
输入的第一行包含两个正整数 $n,m$,表示玩具小人的个数和指令的条数。
接下来 $n$ 行,每行包含一个整数和一个字符串,以逆时针为顺序给出每个玩具小人的朝向和职业。其中 $0$ 表示朝向圈内,$1$ 表示朝向圈外。 保证不会出现其他的数。字符串长度不超过 $10$ 且仅由小写字母构成,字符串不为空,并且字符串两两不同。整数和字符串之间用一个空格隔开。
接下来 $m$ 行,其中第 $i$ 行包含两个整数 $a_i,s_i$,表示第 $i$ 条指令。若 $a_i=0$,表示向左数 $s_i$ 个人;若 $a_i=1$,表示向右数 $s_i$ 个人。 保证 $a_i$ 不会出现其他的数,$1 \le s_i < n$。
输出格式
输出到标准输出。
输出一个字符串,表示从第一个读入的小人开始,依次数完 $m$ 条指令后到达的小人的职业。
7 3
0 singer
0 reader
0 mengbier
1 thinker
1 archer
0 writer
1 mogician
0 3
1 1
0 2
writer
这组数据就是题目描述中提到的例子。
10 10
1 c
0 r
0 p
1 d
1 e
1 m
1 t
1 y
1 u
0 v
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4
y
限制与约定
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
| 测试点 | $n$ | $m$ | 全朝内 | 全左数 | $s_i=1$ | 职业长度为$1$ |
|---|---|---|---|---|---|---|
| 1 | $=20$ | $=10^{3}$ | √ | √ | √ | √ |
| 2 | × | |||||
| 3 | √ | × | ||||
| 4 | × | |||||
| 5 | √ | √ | × | |||
| 6 | × | |||||
| 7 | √ | × | ||||
| 8 | × | |||||
| 9 | √ | √ | √ | × | ||
| 10 | × | |||||
| 11 | √ | × | ||||
| 12 | × | |||||
| 13 | √ | √ | × | |||
| 14 | × | |||||
| 15 | √ | × | ||||
| 16 | × | |||||
| 17 | $=10^{5}$ | $=10^{5}$ | √ | √ | ||
| 18 | × | |||||
| 19 | √ | × | ||||
| 20 | × |
其中一些简写的列意义如下:
- 全朝内:若为“√”,表示该测试点保证所有的玩具小人都朝向圈内;
- 全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 $1 \le i \le m$,$a_i = 0$;
- $s_i=1$:若为“√”,表示该测试点保证所有的指令都只数 $1$ 个,即对任意的 $1 \le i \le m$,$s_i = 1$;
- 职业长度为$1$:若为“√”,表示该测试点保证所有玩具小人的职业一定是一个长度为 $1$ 的字符串。
时间限制:$1\texttt{s}$
空间限制:$512\texttt{MB}$
