uoj#P159. 【清华集训2015】多边形下海
【清华集训2015】多边形下海
在一个二维空间中,给定一个凸多边形,假设该凸多边形的面密度为 $ \rho $ , 放入一个 水平面为 $ y=0 $ 的无穷大的水池当中,水的密度为 $ 1 $ ,求该凸多边形在静止并且势能到达最低点的情况下, 该凸多边形逆时针旋转了多少?
势能包括凸多边形本身的重力势能和浮力对其做功产生的浮力势能。
输入格式
第一行一个数 $N$ ,表示数据组数。 对于每组数据: 第一行两个数,整数 $n$ 和 浮点数 $ \rho $, 表示多边形点的个数和多边形的密度。 接下来 $n$ 行, 每行两个浮点数 $x, y$ 逆时针表示凸包上的所有点。
输出格式
对于每一组数据输出一行,$\theta$, 表示凸多边形达到势能的最低点的时候,其逆时针旋转的弧度是 多少,$ 0 \leq \theta < 2\pi $。
本题包含 Special Judge, 对于你的输出允许 $ 10^{-6} $ 的误差,请输出小数部分位数尽量多的数(但小数位数不要超过 $15$)。
样例一
输入
3 3 0.3 0.23272177 0.50274749 0.69314977 0.57621227 0.63404493 0.80356643 7 0.7 0.97651045 0.03790015 0.9919297 0.75416081 0.76345204 0.83482219 0.17087067 0.83086959 0.19621027 0.49532965 0.24676201 0.45389929 0.67563998 0.14424922 8 0.6 0.03726264 0.10180906 0.50450581 0.13303585 0.81055071 0.29025366 0.99405094 0.68868719 0.77510244 0.87181985 0.40531889 0.91965237 0.27990499 0.84662178 0.07581749 0.30329282
输出
2.60634462 3.83816499 2.50530629
解释
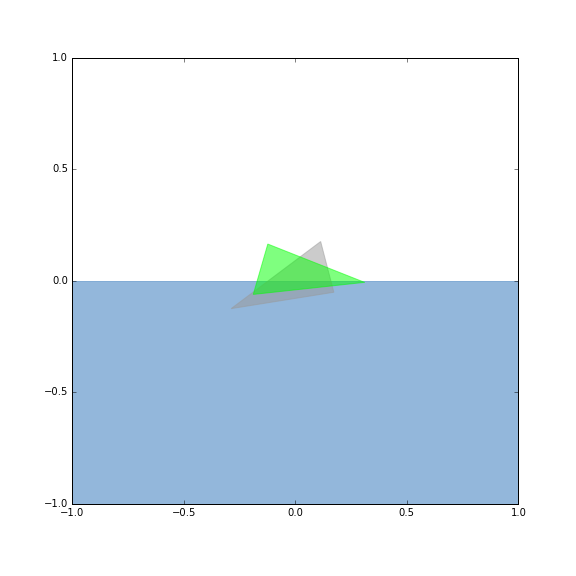
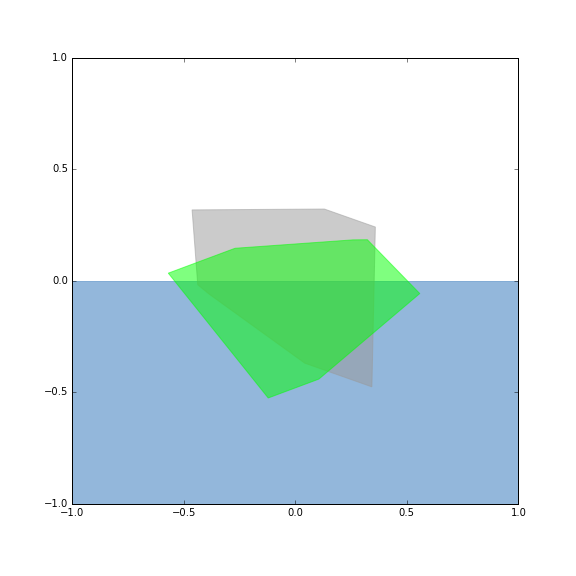
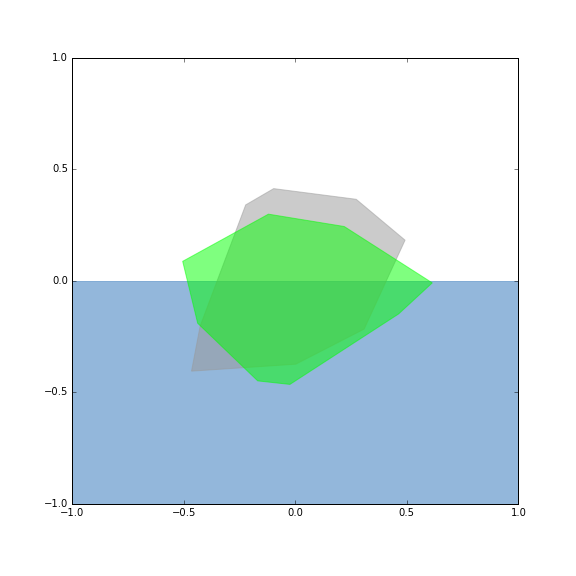
以上三组数据的可视化结果分别如下:
- 绿色代表静止的多边形能量最低时的形态,
- 灰色代表原始多边形,
- 蓝色为水面
限制与约定
时间限制:$1\texttt{s}$
空间限制:$256\texttt{MB}$
凸多边形由逆时针给出。
数据组数 $ N \leq 10 $。
$ 0.1 < \rho < 0.9 $。
$ 0 \leq x,y \leq 1 $。
对于 30% 的数据, $n=3$;
对于 60% 的数据, $n \leq 100$;
对于 100% 的数据, $n \leq 100000$, $ \sum n \leq 100000 $。
数据保证能构成凸多边形,且多边形上相邻两点之间的距离不小于 $10^{-10}$,且多边形的面积不小于 $10^{-4}$。
数据保证唯一解
