luogu#P9701. [GDCPC2023] Classic Problem
[GDCPC2023] Classic Problem
题目描述
Given an undirected complete graph with vertices and triples where , it's guaranteed that , and for any two triples and with different indices we have .
For any two vertices and in the graph (), define the weight of the edge connecting them as follows:
- If there exists a triple satisfying and , the weight of edge will be .
- Otherwise, the weight of edge will be .
Calculate the total weight of edges in the minimum spanning tree of the graph.
输入格式
There are multiple test cases. The first line of the input contains an integer () indicating the number of test cases. For each test case:
The first line contains two integers and (, ) indicating the number of vertices in the graph and the number of triples.
For the following lines, the -th line contains three integers , and (, ) indicating the -th triple. It's guaranteed that for all we have .
It's guaranteed that the sum of of all test cases will not exceed .
输出格式
For each test case output one line containing one integer indicating the total weight of edges in the minimum spanning tree of the graph.
题目大意
【题目描述】
给定一张 个点的无向完全图与 个三元组 ,其中 。保证 ,且对于任意两个编号不同的三元组 和 ,有 。
对于图中的任意两个节点 与 (),定义它们之间的无向边的边权如下:
- 如果存在一个三元组 满足 且 ,那么边权为 。
- 否则,边权为 。
求这张图的最小生成树的边权之和。
【输入格式】
有多组测试数据。第一行输入一个整数 ()表示测试数据组数。对于每组测试数据:
第一行输入两个整数 和 (,)表示图的点数与三元组的数量。
对于接下来 行,第 行输入三个整数 , 和 (,)表示第 个三元组。保证对于所有 都有 。
保证所有数据 之和不超过 。
【输出格式】
每组数据输出一行一个整数,表示这张图的最小生成树的边权之和。
【样例解释】
第一组样例数据如下图所示,最小生成树用红色线段标出。
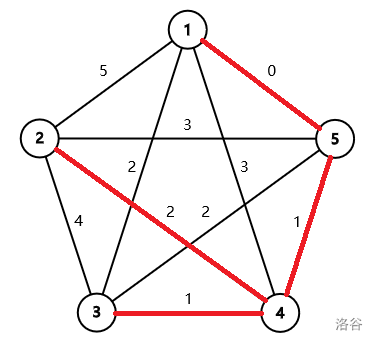
第二组样例数据如下图所示,最小生成树用红色线段标出。
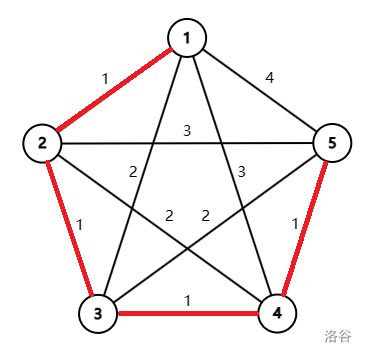
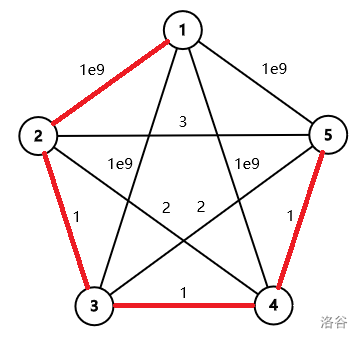
第三组样例数据如下图所示,最小生成树用红色线段标出。
3
5 3
1 2 5
2 3 4
1 5 0
5 0
5 4
1 2 1000000000
1 3 1000000000
1 4 1000000000
1 5 1000000000
4
4
1000000003
提示
The first sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.

The second sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.

The third sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.

