题目描述

BaoBao is playing the famous game $\textit{Elden Ring}$ these days. It's an open-world game in which you can control your character to travel from places to places. However, your character could also enter a trap and you need to figure out how to escape. Right now, BaoBao's character is stuck in a 2-dimensional plane with deadly lasers. There are $n$ laser generators (each can be regarded as a point) shooting laser beams between every pair of them (so there are $\frac{n(n-1)}{2}$ laser beams in total). The beams start and end at generator points and do not stretch to infinity.

Starting at point $(0,0)$, BaoBao wants to escape to point $(10^{10^{10^{10^{10}}}}, 10^{10^{10^{10^{10}}}})$ without touching any laser beam or generator. In order to do so, BaoBao can ask her friend DreamGrid to remove any number of laser generators, together with any laser beam that starts or ends at these generators. Output the minimum number of laser generators that need to be erased for the escape.

Note that BaoBao does not need to move in a specific direction to escape. Her escaping route can even be a curve if necessary.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ indicating the number of test cases. For each test case:

The first line contains an integer $n$ ($1 \le n \le 10^6$) indicating the number of laser generators.

For the following $n$ lines, the $i$-th line contains two integers $x_i$ and $y_i$ ($-10^9 \le x_i, y_i \le 10^9$) indicating the location of the $i$-th laser generator.

It is guaranteed that no two generators coincide, and no laser beam or generator will touch $(0,0)$.

It is also guaranteed that the sum of $n$ of all test cases will not exceed $10^6$.

输出格式

For each test case output one line containing one integer indicating the minimum number of generators that need to be removed.

题目大意

一直角坐标系中，BaoBao 在原点位置，平面上有 $n$ 个发射装置，任意两个发射器之间都有激光束，共 $(n-1) \times n / 2$ 条激光，BaoBao 的朋友可以去除任何发射器，问最少去除多少发射器，能使 BaoBao不会被激光所伤还能从 $(0,0)$ 逃逸到 $\left(10^{10^{10^{10^{10}}}}, 10^{10^{10^{10^{10}}}}\right)$。

tip.发射器不会重合，也不会存在激光束穿过 $(0,0)$。

3
2
1 0
2 0
3
1 0
0 1
-1 -1
5
2 -1
1 2
-1 2
-2 -1
0 -2

0
1
2

提示

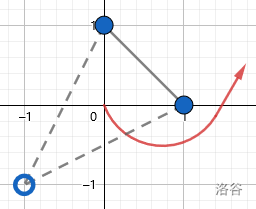
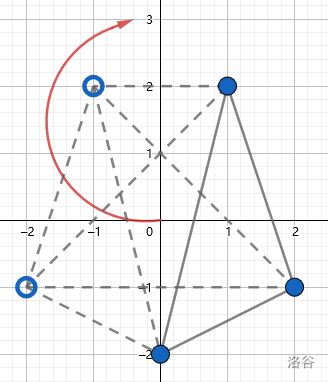
The second and the third sample test cases are shown below. Solid dots and lines represent the remaining laser generators and beams, while hollow dots and dashed lines represent the removed laser generators and beams. The arrow is the escaping route.