luogu#P8493. [IOI 2022] 数字电路
[IOI 2022] 数字电路
题目背景
滥用评测资源者封号。
由于技术限制,请不要使用 C++ 14 (GCC 9) 提交本题。
这是一道交互题,你只需要实现代码中要求的函数。
你的代码不需要引用任何额外的头文件,也不需要实现 main 函数。
由于本题数据点过多,结合洛谷评测技术实现情况,本题将不按照题给 Subtask 评分。
题目描述
有一个数字电路,由编号为从 到 的 个门组成。其中, 到 号门是阈值门,而 到 号门是输入门。
除 号门之外的每个门都是恰好一个某阈值门的输入。具体来说,对于每个满足 的 ,门 是门 的一个输入,其中 。重要的是,我们保证 成立。此外,我们假设有 。每个阈值门有一个或多个的输入。输入门没有任何输入。
每个门都有一个状态,取 或 。输入门的初始状态由一个包含 个整数的数组 给定。也就是说,对于每个满足 的 ,输入门 的初始状态为 。
每个阈值门的状态取决于它的输入的状态,具体如下。首先,每个阈值门会被指定一个阈值参数。对于一个有 个输入的阈值门,其所指定的参数必须是 到 之间的某个整数(包括 和 )。随后,对于一个参数为 的阈值门,如果它的输入中至少有 个门的状态为 ,则当前阈值门的状态为 ,否则状态为 。
例如,假设有 个阈值门和 个输入门。其中,门 的输入为门 和门 ,门 的输入为门 、 和 ,门 仅有的输入为门 。
上述例子的说明可见下图。
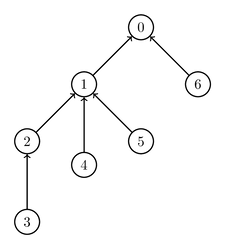
假设输入门 和 的状态为 ,而门 和 的状态为 。假设阈值门 、、 被指定的参数分别为 、、。在这种情况下,门 的状态为 ,门 的状态为 ,门 的状态为 。下面给出了参数赋值以及状态的示意图。状态为 的门被标记为黑色。
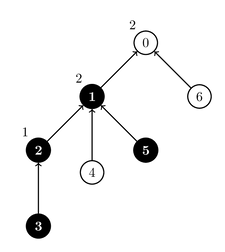
输入门的状态将会经历 次更新。每次更新用两个整数 和 来描述 () ,表示翻转所有编号在 和 之间(包括 和 )的输入门的状态。这就是说,对于所有满足 的 ,输入门 的状态如果为 ,则会被翻转为;如果状态为 ,则会被翻转为 。每个门被翻转后将会一直保持在新状态,直到在后续某次更新中被翻转。
你的目标是,计算每次更新后有多少种阈值门参数的赋值方案,使得门 的状态为 。当有至少一个阈值门的参数不同时,两种参数赋值方案被认为是不同的。由于方案数可能较大,你需要计算它对 取模的结果。
注意,在上面的例子中,共有 种不同的对阈值门参数进行赋值的方案,因为门 、、 分别有 、、 个输入。在这 种方案里面,有 种参数赋值方案使得门 的状态为 。
输入格式
你的任务是实现下述两个函数。
void init(int N, int M, int[] P, int[] A)
- : 阈值门的数量。
- :输入门的数量。
- : 一个长度为 的数组,给出阈值门的输入。
- : 一个长度为 的数组,给出输入门的初始状态。
- 这个函数被调用恰好一次,且发生在函数
count_ways的所有调用之前。
int count_ways(int L, int R)
- , :编号在 和 之间的输入门的状态将会被翻转。
- 这个函数应首先执行所规定的更新,然后返回使得门 的状态为 的参数赋值方案的方案数对 取模的结果。
- 这个函数会被调用恰好 次。
输出格式
考虑如下的函数调用序列:
init(3, 4, [-1, 0, 1, 2, 1, 1, 0], [1, 0, 1, 0])
题面描述中已经给出了对这个例子的解释。
count_ways(3, 4)
这次调用翻转了门 和 的状态,也就是说,门 的状态变成 ,门 的状态变成 。下面给出了两种可行的参数赋值方案,可以使得门 的状态为 。
| 方案 | 方案 |
|---|---|
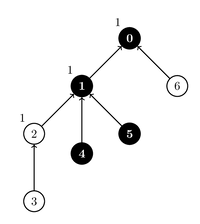 |
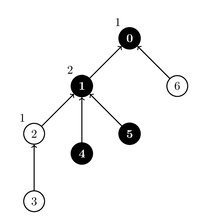 |
在所有其他的参数赋值方案中,门 的状态为 。因此,函数应返回 。
count_ways(4, 5)
这次调用翻转了门 和 的状态。其结果是,所有输入门的状态均为 ,而且对于所有的参数赋值方案,门 的状态均为 。因此,函数应返回 。
count_ways(3, 6)
这次调用将所有输入门的状态置为 。其结果是,对于所有参数赋值方案,门 的状态均为 。因此,函数应返回 。
提示
约束条件
- ;
- ;
- ;
- 且 (对于所有满足 的 );
- 每个阈值门至少有一个输入(对于所有满足 的 ,存在某个下标 满足 且 );
- (对于所有满足 的 );
- 。
子任务
- (2 分),,;
- (7 分),,每个阈值门都有恰好两个输入;
- (9 分),;
- (4 分),(对于某个正整数 ), (对于所有满足 的 ),;
- (12 分),(对于某个正整数 ),(对于所有满足的 );
- (27 分)每个阈值门都恰好有两个输入;
- (28 分);
- (11 分)没有额外的约束条件。
评测程序示例
评测程序示例读取如下格式的输入:
- 第 行: ;
- 第 行: ;
- 第 行: ;
- 第 行(): 第 次更新对应的 。
评测程序示例按照如下格式打印你的答案:
- 第 行():
count_ways函数对第 次更新的返回值。
约定
题面在给出函数接口时,会使用一般性的类型名称 void、bool、int、int[](数组)和 union(bool, int[])。
在 C++ 中,评测程序会采用适当的数据类型或实现,如下表所示:
void |
bool |
int |
int[] |
|---|---|---|---|
void |
bool |
int |
std::vector<int> |
union(bool, int[]) |
数组 a 的长度 |
|---|---|
std::variant<bool, std::vector<int>> |
a.size() |
C++ 语言里,std::variant 定义在 <variant> 头文件中。
一个返回类型为 std::variant<bool, std::vector<int>> 的函数可以返回一个 bool 或一个 std::vector<int>。
以下示例代码给出了三个返回 std::variant 的函数,它们都能正常工作:
std::variant<bool, std::vector<int>> foo(int N) {
return N % 2 == 0;
}
std::variant<bool, std::vector<int>> goo(int N) {
return std::vector<int>(N, 0);
}
std::variant<bool, std::vector<int>> hoo(int N) {
if (N % 2 == 0) {
return false;
}
return std::vector<int>(N, 0);
}
