luogu#P8345. 「Wdoi-6」华胥之梦
「Wdoi-6」华胥之梦
题目背景
题目描述
简要题意
给定长度为 的序列 和常数 。构造点数为 的有向完全图 使得边 ()的长度为 ,保证所有边权非负。
接下来给出 次询问,每次给出一个点集,试找出图 的一条最短的简单路径,满足其经过点集中所有点,并输出它的长度。
原始题意
梅莉做了一个梦,梦到自己穿越到了幻想乡的迷途竹林之中。醒来之后,她希望能够和莲子一起再次穿越境界,进入幻想乡。
但是,这一次,她看到了 个世界,其中,第 个世界的结界强度为 。而世界之间两两都有通道相连,莲子和梅莉便是通过这些通道来进行世界之间的穿梭的。
为了避免错过幻想乡所在的世界,因此她们每到达一个世界,都会穿越结界。莲子和梅莉从第 个世界中,通过一条通道,再穿越结界进入第 个世界,需要使用的灵能为 (保证所需消耗的灵能非负),其中 是一个常数,是梅莉每次穿越结界需要的额外灵能消耗。注意,这也意味着,从第 个世界到第 个世界,与第 个世界穿越到第 个世界所消耗的灵能,可能是不同的。
为了能够高效地找到幻想乡,她们会对你进行 次询问,每次询问的时候会给出一个集合,表示她们想要进入的世界。由于世界众多,她们希望能够节省灵能,因此她希望你能求出所有包含这些世界的简单路径(即:同一条世界间的通道不会被走多次)中,消耗灵能值之和最少的路径。你只需告诉她们消耗灵能值之和最少为多少。
输入格式
- 第一行三个整数 。
- 第二行 个整数表示数列 。
- 接下来 行。每行第一个整数 ,即集合 的大小。后面 个互不相同的整数表示集合 。
输出格式
- 输出共 行,每行一个整数,表示询问的答案。
5 20 3
7 4 2 5 9
2 1 4
3 1 2 3
4 1 4 2 5
11
24
34
10 928698067 3
331485039 15480787 61584781 252174726 472089427 95998831 252561792 118119945 315548522 24453837
4 9 1 10 2
5 10 6 1 5 8
1 5
1798602551
2249463436
0
提示
样例解释
样例 #1
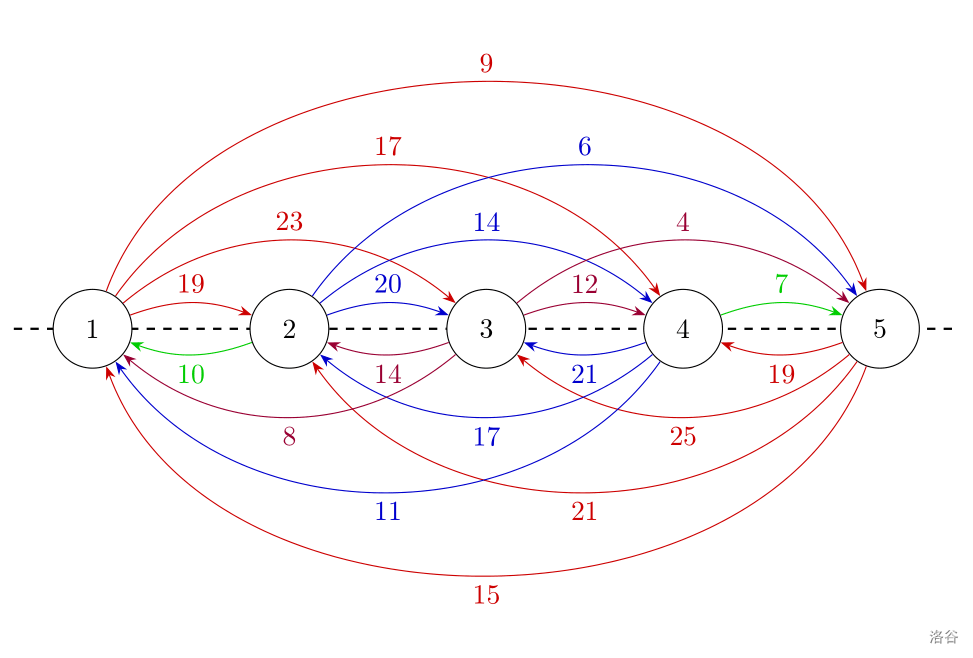
每两个点之间的边权如图所示。为了便于选手观察,边权的颜色与它所对应的边的颜色相同。
对于第一个询问,可以找到路径 ;对于第二个询问,可以找到路径 ;对于第三个询问,可以找到路径 。可以证明,这三个方案分别是对应询问的最优方案。
样例 #2
该样例符合 的限制。
数据范围
本题采用捆绑测试。
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{\textsf{分值}} & \bm{n\le } & \bm{q\le} & \bm{\sum |S|\le} & \textbf{\textsf{特殊性质}}&\textbf{Subtask \textsf{依赖}}\cr\hline 1 & 30 & 10 & 10 & 10 & - &-\cr\hline 2 & 20 & 10^5 & 10^5 & 10^5 & \mathbf{A}&- \cr\hline 3 & 20 & 10^5 & 10^5 & 10^5 & \mathbf{B}&- \cr\hline 4 & 30 & 10^6 & 10^6 & 10^6& -&1,2,3 \cr\hline \end{array} $$- 特殊性质 : 单调递增。
- 特殊性质 : 全部相等。
对于 的数据,保证 $1 \leq S_i \leq n \leq 10^6, 1\leq \sum |S|,q \leq 10^6, 1 \le a_i,c \le 10^9$。

