luogu#P6889. [CEOI 2006] CONNECT
[CEOI 2006] CONNECT
题目描述
Back in the day when the famous sixteen-bit three-letter operating system most often used on an 25x80 terminal dominated the PC market, "Nibbles" was everyone's favorite computer game. This problem, however, is not related to Nibbles – it is related to a game called "Connect" which is almost, but not quite, entirely unlike Nibbles.
Connect is played on a board composed of squares organized into R rows and columns, where both and are odd numbers. Rows and columns are numbered to and to , respectively. Each position on the board is either free or blocked by a wall. Additionally, each board satisfies the following constraints:
- Squares with both coordinates even are called rooms. They are never blocked.
- Squares with both coordinates odd are called barriers. They are always blocked
- All other squares are called corridors. They may or may not be blocked.
- Corridors along the edge of the board are always blocked.
Barriers are represented by the '+' (plus) character, blocked horizontal corridors by the '|' (pipe) character, while blocked vertical corridors are represented by the '–' (minus) character. Rooms and free corridors are represented by the blank character.
At the beginning of the game an even number of figures (represented by the uppercase letter 'X') are placed on the board – each in a separate room. path between figures and is a sequence of free squares starting from , ending with and moving in one of the four possible directions in each step (the path includes both endpoint squares, and ). The length of the path is the total number of steps needed to get from to (which is equal to the number of squares contained in the path minus one).
The goal of the player is to first divide all the figures into pairs, and then, for each pair, connect the two figures with a path. The pairs should be connected in such a way that no two paths share a common square.
For a completed game, the score is defined as the sum of the lengths of all paths.
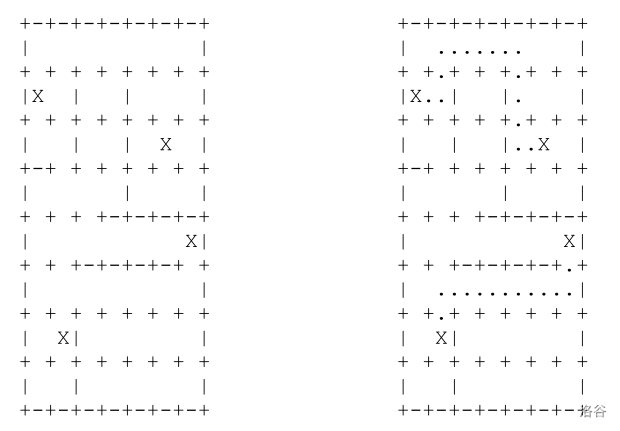
Write a program that, given the starting position of the Connect game, plays the game in such a way that the minimum possible score is achieved. The test data will guarantee that a solution, although not necessarily unique, will always exist.
输入格式
第一行输入为两个整数: 与 ,其中 为行数, 为列数, , 均为奇数。
接下来的 行每行包括 个字符,每个字符都是+、|、- 、空格或X中的一个,分别表示障碍及两种墙壁、空格表示房间或可通过的走廊,X表示房间中的物品。
输出格式
输出的第一行是一个整数,即最小分值。
本题不要求输出合法方案
题目大意
给定一个 大小的迷宫,其中 均为奇数。
迷宫中两个- 坐标值均为奇数的点不能通过,称为障碍;迷宫中其他不能通过的点统称为墙壁;坐标为两个偶数的点可以通过,称为房间;迷宫中其他可通过的点称为走廊。
迷宫有边界,迷宫中放置有偶数个物品,物品一定放置在房间中,问如何将这些物品配对可以使得所有物品对之间路径的总和最小,任两条路径不能相交,并输出这个总和的最小值。
17 15
+-+-+-+-+-+-+-+
| |
+ + + + + + + +
|X | | |
+ + + + + + + +
| | | X |
+-+ + + + + + +
| | |
+ + + +-+-+-+-+
| X|
+ + +-+-+-+-+ +
| |
+ + + + + + + +
| X| |
+ + + + + + + +
| | |
+-+-+-+-+-+-+-+
30
提示
,
