luogu#P6888. [CEOI2006] Walk
[CEOI2006] Walk
题目描述
Finding your destination in a big unknown city can be challenging, especially if you are a computer scientist like Kirk, always trying to use the shortest possible path. Planning can help – given the map of the city Kirk wants to find the shortest path between his current position and his destination.
The map of the city can be represented in the plane as an infinite grid composed of unit squares.
Kirk is currently located at the square (0, 0) and his destination is the square (X, Y).
There are N buildings in the city. Each building is a rectangle fully occupying a number of unit squares. No two buildings touch or overlap, i.e. Kirk can walk freely around every building. A building is defined by specifying the coordinates of two diagonally opposite squares occupied by the building.
In each step, Kirk can walk to one of the four neighboring squares, but he is not allowed to step onto a square occupied by a building. His current position is at the west entrance to the city and the x coordinate of every square occupied by a building is strictly greater than zero.
Write a program that, given the locations of the buildings, finds one shortest possible path from Kirk's current position to his destination. A path should be reported as a sequence of vertical and horizontal segments, with no two consecutive segments parallel. The length of a path is the number of squares contained in the path, excluding the initial square.
输入格式
The first line of input contains two integers X, Y (1 ≤ X ≤ 106, -106 ≤ Y ≤ 106) – the coordinates of the destination square. The second line of input contains a single integer N (0 ≤ N ≤ 100 000) – the number of buildings in the city. Each of the following N lines contains four integers X1, Y1, X2, Y2 (1 ≤ X1, X2 ≤ 106, -106 ≤ Y1, Y2 ≤ 106) – the coordinates of two diagonally opposite squares occupied by the building.
输出格式
The first line of output should contain an integer L – the length of the shortest path to the destination. The second line of output should contain an integer M – the number of segments in the shortest path. The number of segments M must not exceed 1,000,000.
Each of the following M lines should contain two integers, DX and DY, describing Kirk's relative movement in one segment. For each segment, exactly one of the values DX, DY should be zero, and no two consecutive segments should be parallel.
Note: if there are multiple solutions, you should output any one of them.
题目大意
在一个陌生的城市中寻找目的地确实是一项颇具挑战性的任务,特别是对于像 Kirk 这样的计算机科学家而言——他总是试图去寻找一条可能的最短路径。在这种情况下,事先做好规划是有帮助的。Kirk 希望借助这个城市的地图找出他当前所在位置与目标位置之间的最短路径。
用一个平面来表示城市地图,它由很多个单位边长的正方形网格组成。
Kirk当前所处位置为方格 ,而他的目标是方格 。
城市中有 个建筑,而且每个建筑是一个完全覆盖了若干个方格的长方形。注意,任意两个建筑之间彼此均互不重叠或互不相交,Kirk 可以随意地围绕任一个建筑走上一圈。建筑用一对坐标来表示,它们是长方形对角线的两个端点。
在每一步中,Kirk 可以朝着四个方向的任意一个方向前进,但是他不能进入被建筑占据的方格。他现在的位置是城市西边的入口,而每个建筑所占据的方格的 坐标均大于 。
试编写一个程序,当给出所有建筑位置时,找出一个从 Kirk 当前位置到目标位置的可能的最短路径。一条路径应该由一系列水平和竖直的线段构成,任意两个相邻线段都不应该平行。路径的长度是路径占据的方格数,初始的那个方格除外。
终点位置 ,,建筑个数 ,建筑物的两点坐标 ,
9 1
2
5 -3 8 3
10 -3 13 3
16
12 0
5
2 -1 3 1
6 -7 8 -1
6 1 8 6
4 3 4 5
10 -5 10 3
24
42 33
66
35 37 37 37
13 -41 13 6
40 -2 42 -1
27 -2 28 -2
15 -4 16 2
29 16 29 16
38 -34 38 -11
22 -5 22 -5
34 27 34 35
28 12 29 12
10 11 11 13
11 25 11 25
24 4 25 40
27 9 27 10
27 -4 27 -4
29 7 29 10
3 -13 5 -13
16 17 16 17
18 6 18 48
4 7 4 14
5 2 5 5
40 22 44 32
21 13 21 13
34 3 34 25
41 11 42 20
15 -15 16 -9
24 -46 25 -6
5 -4 5 -3
10 17 11 17
28 14 29 14
3 -15 4 -15
10 15 10 15
16 8 16 9
2 2 2 2
1 -4 3 -3
10 21 10 21
22 8 22 8
20 -3 21 2
10 19 11 19
7 -47 8 3
28 -11 28 -6
20 4 20 9
11 23 11 23
15 -17 16 -17
27 0 27 3
43 5 43 8
15 -7 16 -6
16 -19 16 -19
11 -10 11 -10
21 11 22 11
4 0 4 0
15 5 16 6
3 -11 5 -7
11 -8 11 -1
28 -13 28 -13
21 15 22 15
40 -30 43 -5
41 34 43 35
15 14 16 15
21 -16 22 -13
1 -1 2 -1
10 1 11 9
22 17 22 17
31 -50 32 -1
22 -8 22 -7
16 -21 16 -21
89
提示
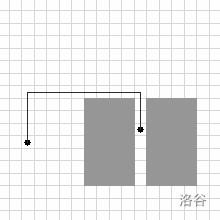
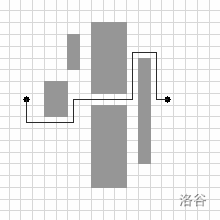
Note: each of the figures depicts the respective input, along with the supplied solution.
注意:原题还要求输出方案,本题略去。
