题目描述

The protagonist of this task, Chell, must solve a new puzzle GLaDOS has come up with.

Chell is in a room whose layout that can be represented as a matrix of dimensions N rows and M columns. Each field can be one of the following:

• Obstructed field - there is a wall in it (denoted as ‘#’),
• The field where Chell is initially (denoted as ‘C’),
• The field where Chell must get to in order to solve the puzzle (denoted as ‘F’), or
• An empty field (denoted as ‘.’).

Chell is carrying a so-called portal gun, a gun with which you can create portals in the walls.

In each move, she can do one of the following:

• Move to an adjacent field using one move up, down, left or right (she cannot move to the field with a wall in it). This move lasts one unit of time.
• Create a portal in the wall by turning towards a wall, not necessarily an adjacent one, in the direction up, down, left or right and shooting. The portal will be created only on the side of the wall it was hit from. In each moment, at most two portals can be active​. If a new portal is being created in the moment when two portals are already active, the one that was created earlier will disappear. It is not possible to create a new portal at the position of another existing portal. This move lasts a negligible amount of time, i.e. zero amounts of time.
• If she’s at a field that is adjacent to a wall and there’s a portal on her side of the wall, she can step into the portal and exit to a non-obstructed field with another portal. This move is possible if there are two active portals and lasts one unit of time.

Chell wants to know the minimal amount of time it takes for her to solve the puzzle, i.e. to reach the field denoted as ‘F’.

Please note: The room will always have walls on the sides, and letters ‘C’ and ‘F’ will appear only once in the matrix.

输入格式

The first line of input contains the positive integers N and M (4 ≤ N, M ≤ 500), the numbers from the task.

Each of the following N lines contains M characters that describe the layout of the room.

输出格式

You must output the minimal amount of time it takes to solve the puzzle, or “nemoguce” (without quotation marks, Croatian for impossible) if it is not possible to solve it.

题目大意

题目大意:

给定一个矩阵，每个格子由下列字母表示：

●有障碍的区域表示为‘#’

● 初始位置表示为‘C’

● 目标位置表示为 ‘F’

● 空白区域表示为‘.’

可以进行三种操作： ●走到上下左右相邻的格子，不能走到有墙的区域上，消耗一个单位时间。

●在墙壁上创建传送门，用枪向上、向下、向左，向右直射向着墙壁。传送门会在被击中的墙的一侧产生。在每一时刻，最多两个传送门可以是活动的。如果在已有两个传送门的基础上再射击创建了一个新的，那么较早创建的门将消失。这个射击消耗的时间可忽略。

●如果她在一个靠近墙的地方，墙上有一个传送门，她可以进入，到达另一个门外的无障碍区域出来，需要消耗一个单位时间。

求到达目的地“F”所需的最少时间

4 4
####
#.F#
#C.#
####

2

6 8
########
#.##..F#
#C.##..#
#..#...#
#.....##
########

4

4 5
#####
#C#.#
###F#
#####

nemoguce

提示

In test cases worth 50% of total points, it will hold 4 ≤ N, M ≤ 15.

Clarification​ ​of​ ​the​ ​second​ ​test​ ​case:

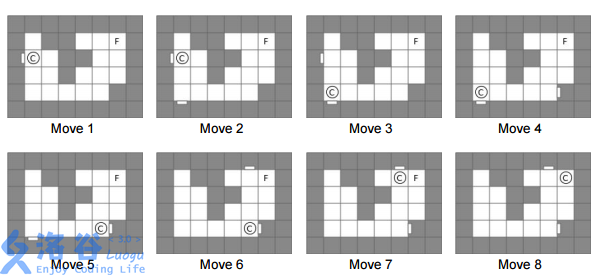
The puzzle can be solved in 8 moves, illustrated in the pictures below.

In the first move, we turn towards the left wall, shoot and create a portal that appears on the wall in the $3^{rd}$ row and $1^{st}$ column (coordinates (3,1)) from the right side.

In the second move, we create a portal from the upper side of the wall at coordinates (6,2).

In the third move, we step into the portal at coordinates (3,1) and exit at coordinates (5,2) - a non-obstructed field with the second portal.

In the fourth move, we turn right and create a portal from the left side of the wall at coordinates (5,7). Since there are already two portals, the one at field (3,1) disappears.

In the fifth move, we step into the portal at coordinates (6,2) and exit at coordinates (5,6) with the second portal.

In the sixth move, we create a new portal from the lower side of the wall at coordinates (1,6), making the portal at coordinates (6,2) disappear.

In the seventh move, we step into the portal at coordinates (5,7) and exit at coordinates (2,6). Finally, in the eighth move, we move one place to the right to end the game.

The portal creation in moves 1, 2, 4 and 6 lasts zero amounts of time, whereas the rest of the move last one unit of time, so the total time needed to solve the puzzle is 4 units of time.