题目描述
给定方程
x1+x2+⋯+xn=m。
我们对第 1∼n1 个变量进行一些限制: $x_{1} \le a_{1},x_{2} \le a_{2},\dots, x_{n_1} \le a_{n_1}$。
我们对第 n1+1∼n1+n2 个变量进行一些限制: $x_{n_1+1} \ge a_{n_1+1},x_{n_1+2} \ge a_{n_1+2},\dots,x_{n1+n2} \ge a_{n_1+n_2}$。
求:在满足这些限制的前提下,该方程正整数解的个数。答案可能很大,请输出对 p 取模后的答案。
输入格式
输入含有多组数据。
第一行两个正整数 T,p。T 表示这个测试点内的数据组数,p 的含义见题目描述。
对于每组数据,第一行四个非负整数 n,n1,n2,m。
第二行 n1+n2 个正整数,表示 a1,a2,…,an1+n2。请注意,如果 n1+n2 等于 0,那么这一行会成为一个空行。
输出格式
共 T 行,每行一个正整数表示取模后的答案。
3 10007
3 1 1 6
3 3
3 0 0 5
3 1 1 3
3 3
3
6
0
提示
【样例解释】
对于第一组数据,三组解为 (1,3,2),(1,4,1),(2,3,1)。
对于第二组数据,六组解为 (1,1,3),(1,2,2),(1,3,1),(2,1,2),(2,2,1),(3,1,1)。
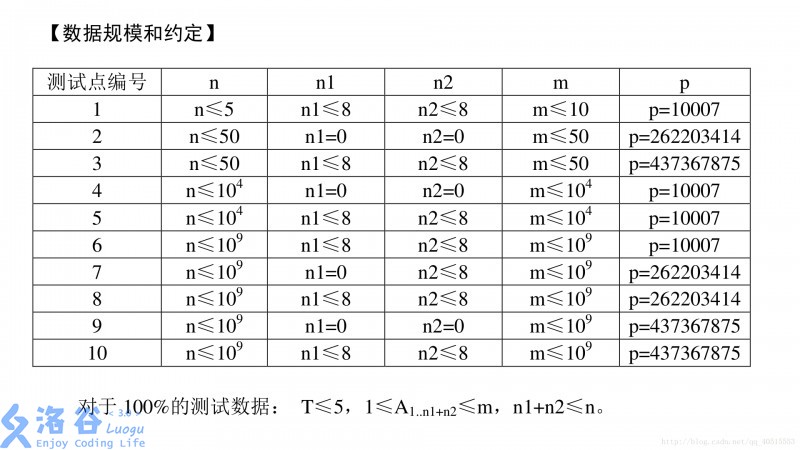
对于 100% 的数据,1≤T≤5,1≤m,n≤109,1≤ai≤m,0≤n1,n2≤min(8,m) 且 n1+n2≤n,1≤p≤437367875。

