题目描述

The Scientific Committee is planning to visit $n$ cities. The $n$ cities are connected by exactly $n - 1$ roads such that it is possible to move between all pairs of cities using the roads. Road $i$ is built between cities $u[i]$ and $v[i]$.

Each city has its own airport. To begin the trip, the committee will fly from Singapore to one of the cities. To make the most out of their trip in the most efficient way possible, the committee wants to visit each city at least once by using each road exactly twice (once in each direction), before flying back home from the last city they find themselves in. A trip satisfying this condition is called a tour.

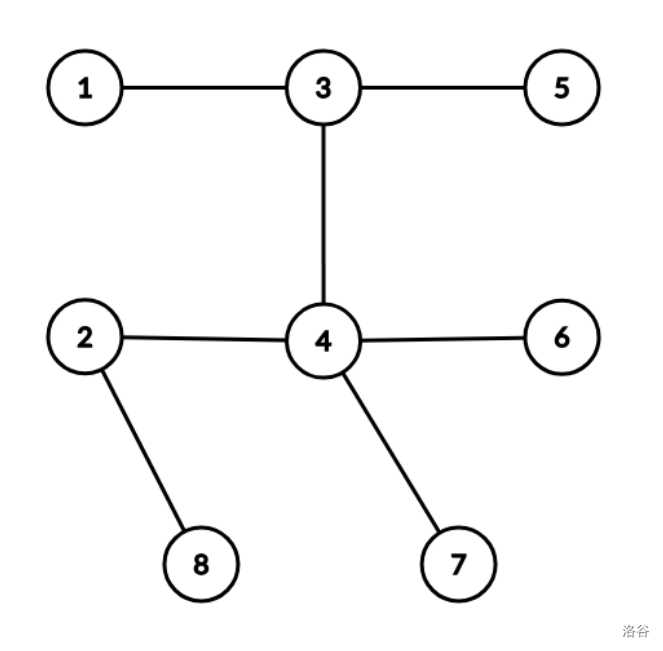
For example, let the diagram above represent a map of $n = 8$ cities. One possible tour starting from city $1$ is $1 \to 3 \to 5 \to 3 \to 4 \to 2 \to 8 \to 2 \to 4 \to 6 \to 4 \to 7 \to 4 \to 3 \to 1$. Observe that this tour visits all cities a total of $2n - 1$ (equal to $15$) times and ends at the same city it started from (city $1$). It can be shown that these two properties are true for all tours in all possible maps of cities.

The committee also wants to visit $m$ events which will happen in order from event $1$ to event $m$. Event $j$ will be held in city $s[j]$. A city can hold zero, one or multiple events, but no two consecutive events are held in the same city, i.e., $s[j] = s[j + 1]$.

A tour that allows the committee to visit all events must visit the cities $s[1], s[2], \ldots, s[m]$ in order, not necessarily consecutively. Such a tour is called an itinerary. Formally, let $t[1], t[2], \ldots, t[2n - 1]$ be the sequence of cities visited in some tour. A tour is an itinerary if and only if $s$ is a subsequence of $t$. That is, $s$ can be obtained by deleting zero or more elements from $t$ and maintaining the order of the remaining elements. Using the same example as above, suppose that $m = 4$ and $s = [3, 5, 2, 7]$, then the tour $1 \to \textbf{3} \to \textbf{5} \to 3 \to 4 \to \textbf{2} \to 8 \to 2 \to 4 \to 6 \to 4 \to \textbf{7} \to 4 \to 3 \to 1$ above is an itinerary because the cities $3, 5, 2, 7$ are visited in order during the tour (underlined and marked in bold).

The committee is still deciding which city to start from, but they agree that a city is a good choice to start from if there exists an itinerary that starts from it. For all cities, help the committee determine if there exists at least one itinerary starting from that city.

输入格式

Your program must read from standard input.

The first line of input contains two space-separated integers $n$ and $m$, describing the number of cities and the number of events respectively.

The following $n - 1$ lines of input each contain two space-separated integers. The $i$-th of these lines contains $u[i]$ and $v[i]$, describing the endpoints of the $i$-th road.

The last line of input contains $m$ space-separated integers $s[1], s[2], \ldots, s[m]$, describing the cities that are holding events.

输出格式

Your program must print to standard output.

The output should contain $n$ lines. If there exists an itinerary starting from city $i$, then the $i$-th line should contain a single integer $1$. Otherwise, the $i$-th line should contain a single integer $0$.

8 4
1 3
2 4
3 4
4 6
5 3
2 8
7 4
3 5 2 7

1
0
1
1
0
1
1
0

8 4
1 3
2 4
3 4
4 6
5 3
2 8
7 4
3 2 5 7

0
0
0
0
0
0
0
0

4 7
1 2
1 3
1 4
2 1 2 1 2 1 2

0
0
0
0

5 2
1 2
2 3
3 4
4 5
2 4

1
1
1
1
1

提示

Subtasks

For all test cases, the input will satisfy the following bounds:

• $2 \leq n \leq 200\,000$
• $1 \leq m \leq 2n - 1$
• $1 \leq u[i], v[i] \leq n$ for all $1 \leq i \leq n - 1$
• $1 \leq s[j] \leq n$ for all $1 \leq j \leq m$
• $s[j] \neq s[j + 1]$ for all $1 \leq j \leq m - 1$
• It is possible to move between all pairs of cities using the roads.

Your program will be tested on input instances that satisfy the following restrictions:

Subtask	Marks	Additional Constraints
$0$		Sample test cases
$1$	$7$	$n \leq 1000, m = 2n - 1$
$2$	$10$	$u[i] = 1, v[i] = i + 1$
$3$	$6$	$n \leq 1000, u[i] = i, v[i] = i + 1$
$4$	$7$	$u[i] = i, v[i] = i + 1$
$5$	$14$	$n \leq 1000, m \leq 10$
$6$	$5$	$n \leq 1000$
$7$	$19$	$m \leq 10$
$8$	$11$	$s[1] = s[m]$
$9$	$21$	No additional constraints

Sample Test Case 1 Explanation

This test case is valid for subtasks $5, 6, 7$, and $9$.

This test case is described as an example in the problem statement.

There are itineraries starting from cities $1, 3, 4, 6$, and $7$. An itinerary starting from city $1$ is given in the problem statement.

On the other hand, it can be shown that there are no itineraries starting from cities $2, 5$, and $8$.

Sample Test Case 2 Explanation

This test case is valid for subtasks $5, 6, 7$, and $9$.

This test case is the same as the example in the problem statement, except $s[2]$ and $s[3]$ are swapped. No itineraries exist at all.

Sample Test Case 3 Explanation

This test case is valid for subtasks $1, 2, 5, 6, 7, 8$, and $9$.

Sample Test Case 4 Explanation

This test case is valid for subtasks $3, 4, 5, 6, 7$, and $9$.