题目背景

USTCPC 设置 3s 时限为了使得 python 通过。洛谷改为 1s 时限。

2024 年 12 月 28 日 14:59:50，随着最后一发 E 题的提交出现了 Wrong Answer，小 G 的 EC-Final 比赛结束了。

小 G 的 EC-Final 连续两年都在不同的细节题上倒闭了。克露丝卡尔酱想要帮助她的同学小 G！很可惜细节题是不能批量生产的，但刚好克露丝卡尔酱想到了这样一个细节题，考验大家的细节题能力。希望大家不要在细节题上倒闭！

为什么这个系列的题目还在继续呢？

题目描述

给定一个 $n$ 个点，$m$ 条边的无向图。第 $i$ 条边 $(u_i,v_i)$ 有一个未知边权 $a_i$。

对于任何一条路径，定义其代价如下：设路径为 $(p_0,p_1,...,p_k)$，其中要求 $(p_{i-1},p_i)$ 是无向图中的边，设其为第 $e_i$ 条边。那么路径的代价即为 $\mathop{\text{mex}}\limits_{i=1}^{k} a_{e_i}$。（该路径可以经过重复点和重复边，即 $p$ 和 $e$ 可以包含重复的数）

$\text{mex}$ 是一种定义域为一个非负整数的可重集合，函数值为非负整数的映射，定义为集合内最小未在集合内出现过的非负整数。

定义 $f(x,y)$ 为从 $x$ 到 $y$ 的所有路径中代价的最大值。

给定 $n,m$，再对于每条边 $(u_i,v_i)$ 给定 $f(u_i,v_i)$，你需要求出是否存在一组合法的 $a_i$，如果有解，你还需要构造一组解。

输入格式

第一行两个正整数 $n,m$ $(1\le n,m\le 10^5)$。

第 $2\sim m+1$ 行每行两个正整数 $u_i,v_i$ $(1\le u_i,v_i\le n)$ 和一个非负整数 $f(u_i,v_i)$ $(0\le f(u_i,v_i)<2^{31})$。

请注意：本题并不保证图连通；可能会存在重边和自环。

输出格式

如果不存在解，则仅输出 No。

否则，在第一行输出 Yes，在第二行输出 $m$ 个非负整数 $a_i$ 表示一组合法的解。

答案可能有很多组，此时输出任意一组解即可。你需要保证 输出的 $0\le a_i<2^{31}$。

你可以以任意的大小写形式输出 Yes 或 No。例如，yEs，yes，Yes 和 YES 都将被视为肯定的回复。

3 3
1 2 2
2 3 2
3 1 2

Yes
0 1 114514

1 1
1 1 114514

NO

提示

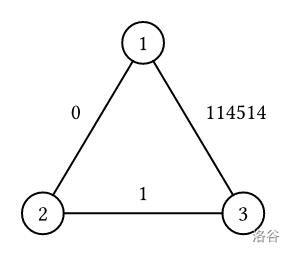
考虑 $f(1,2)$：

• 考虑路径 $1\rightarrow 2$，路径的代价为 $\text{mex}\{0\}=1$。
• 考虑路径 $1\rightarrow 2\rightarrow 3\rightarrow 1\rightarrow 2$，路径的代价为 $\text{mex}\{0,1,114514,0\}=2$。
• 考虑路径 $1\rightarrow 3\rightarrow 2$，路径的代价为 $\text{mex}\{1,114514\}=0$。

此外还存在其他路径，但可以证明不存在代价比 $2$ 更大的路径，故 $f(1,2)=2$。