luogu#P11584. [KTSC 2022 R1] 飞扬的小鸟
[KTSC 2022 R1] 飞扬的小鸟
题目背景
请使用 C++17 或 C++20 提交本题
你需要在程序开头加入如下代码:
#include<bits/stdc++.h>
long long get_max_score(int W, int H, std::vector<int> A, std::vector<int> X1, std::vector<int> Y1, std::vector<int> X2, std::vector<int> Y2);
题目描述
题目译自 2022년도 국제정보올림피아드 대표학생 선발고사 - 1차 선발고사 T2「 플래피 버드 」

你知道 2014 年曾经流行的游戏「Flappy Bird」吗?这是一款游戏,玩家需要控制一只小鸟在前进的过程中避免撞到管道或飞出屏幕,通过不断上升和下降尽可能地飞得更远。
在这个游戏中出现的小鸟其实是教准养的宠物鸟“安娜”。教准和安娜今天也在二维世界中玩类似于「Flappy Bird」的游戏。安娜在天空中飞行,经过线段时会根据线段的权重获得相应的分数。
这个游戏的规则如下: 在二维平面上有 条与 轴或 轴平行的线段。第 条线段的权重为 ,两个端点的坐标分别为 和 。
安娜从 直线上的任意点开始向 方向飞行,当到达 直线时结束飞行。但出于安全考虑,安娜不能飞到 以下或 以上。也就是说,安娜只能在 的区域内飞行。
安娜只能平行于 轴飞行,因此在飞行过程中不能改变自己的 坐标。但她可以在飞行过程中借助教准的帮助,垂直于 轴上升或下降一次,改变自己的 坐标。在上升或下降过程中,安娜的 坐标不变,且只能选择上升或下降其中之一。
安娜的飞行路径与一条或多条线段共享一个或多个点时,这些线段的权重之和就是安娜获得的分数。 例如,假设 ,有 条线段如下图所示。
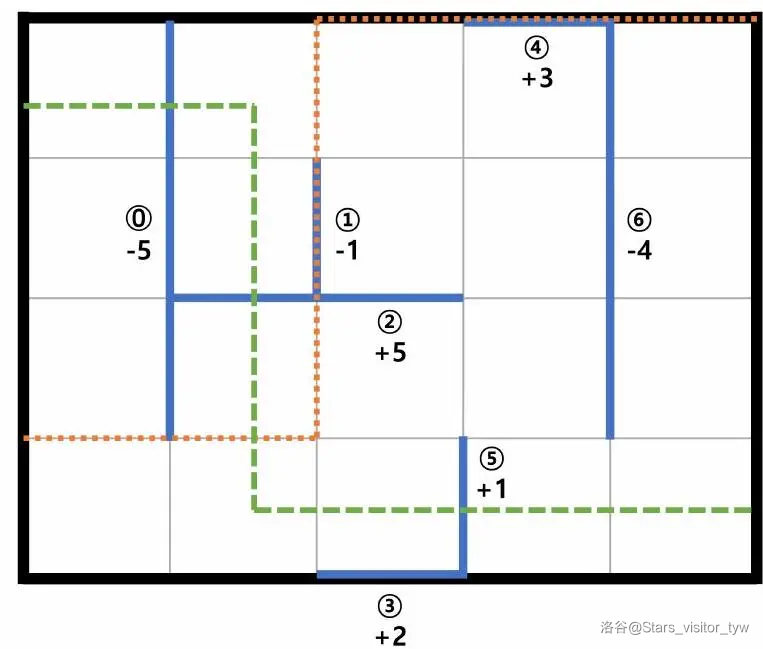
蓝色实线表示线段,虚线表示安娜的飞行路径。圆圈内的数字是线段编号,有符号的数字是权重。 如果安娜从 开始飞行,在 上升到 ,然后在 结束飞行,她会经过第 号线段,获得 分。
但如果安娜从 开始飞行,在 下降到 ,然后在 结束飞行,她会经过第 号线段,获得 分。
给定 条线段的信息,编写一个程序计算安娜可以获得的最大分数。
你需要实现以下函数:
long long get_max_score(int W, int H, vector<int> A, vector<int> X1, vector<int> Y1, vector<int> X2, vector<int> Y2);
- 该函数只会被调用一次。
- 参数中给定的整数数组 的大小为 。数组的每个元素 分别表示 。
注意,提交的代码中不应包含任何输入输出操作。
该函数返回安娜可以获得的最大分数。
输入格式
示例评测程序按以下格式读取输入:
- 第 行:
- 第 行:
输出格式
示例评测程序按以下格式输出:
- 第 行:函数
get_max_score返回的值。
2 1 2
6 1 0 1 1
-10 1 0 1 1
-4
5 4 5
1 1 0 1 2
1 2 1 2 2
1 3 1 3 4
1 1 3 4 3
-1 2 1 4 1
4
11 8 11
1 5 5 5 1
-3 2 4 10 4
0 10 1 8 1
-2 3 3 3 7
2 2 0 2 4
7 7 8 10 8
-1 4 2 1 2
-1 8 3 8 8
-1 7 8 10 8
-2 7 5 7 6
-1 10 5 8 5
5
提示
样例解释 #1
考虑 $W=2, H=1, N=2, A=[6,-10], X_{1}=[1,1], Y_{1}=[0,0], X_{2}=[1,1], Y_{2}=[1,1]$ 的情况。
评测程序将调用如下函数:
get_max_score(2,1,[6,-10],[1,1],[0,0],[1,1],[1,1])=-4
下图显示了 N 条线段和安娜可以获得最大分数的路径。
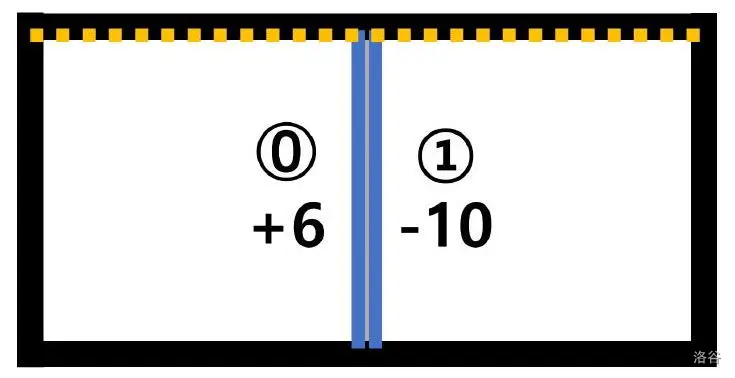
安娜从 开始飞行,不进行上升或下降,在 结束飞行,经过第 和 号线段,获得总分 。
这个例子满足子任务 的条件。
样例解释 #2
考虑 $W=5, H=4, N=5, A=[1,1,1,1,-1], X_{1}=[1,2,3,1,2], Y_{1}=[0,1,1,3,1], X_{2}=[1,2,3,4,4], Y_{2}=[2,2,4,3,1]$ 的情况。
评测程序将调用如下函数:
get_max_score(5, 4, [1, 1, 1, 1, -1],[1,2,3,1,2],[0,1,1,3,1],[1,2,3,4,4],[2,2,4,3,1])=4
这个样例满足子任务 的条件。
样例解释 #3
考虑 $W=11, H=8, N=11, A=[1,-3,0,-2,2,7,-1,-1,-1,-2,-1], X_{1}=[5,2,10,3,2,7,4,8,7,7,10], Y_{1}=[5,4,1,3,0,8,2,3,8,5,5], X_{2}=[5,10,8,3,2,10,1,8,10,7,8], Y_{2}=[1,4,1,7,4,8,2,8,8,6,5]$ 的情况。
评测程序将调用如下函数:
get_max_score(11, 8, [1, -3, 0, -2, 2, 7, -1, -1, -1, -2, -1], [5, 2, 10, 3, 2, 7, 4, 8, 7, 7, 10], [5, 4, 1, 3, 0, 8, 2, 3, 8, 5, 5], [5, 10, 8, 3, 2, 10, 1, 8, 10, 7, 8], [1, 4, 1, 7, 4, 8, 2, 8, 8, 6, 5]) = 5
这个例子满足子任务 的条件。
数据范围
对于所有输入数据,满足:
- 输入中给定的所有数都是整数。
- $1 \leq X_{i, j} \leq W-1 (i \in\{1,2\}, 0 \leq j \leq N-1)$
- $0 \leq Y_{i, j} \leq H (i \in\{1,2\}, 0 \leq j \leq N-1)$
- 对于每个 , 或
- 所有线段的长度都是正数。即,对于每个 ,$\left(X_{1, i}, Y_{1, i}\right) \neq \left(X_{2, i}, Y_{2, i}\right)$
详细子任务附加限制及分值如下表所示。
| 子任务 | 分值 | 约束 |
|---|---|---|
| 无附加限制 |
