题目背景

翻译自 ROIR 2016 D2T1。

题目描述

在王国的领地上，有一条长为 $n$ 公里的直路，道路一侧是一个巨大的森林。国王十分关注自然保护，决定将这片森林设为自然保护区。但是，国王的三个儿子表示反对，因为他们希望能继承这些土地。

国王决定，森林保护区的土地不能继承给儿子。在制定遗嘱时，国王希望分配的土地满足以下条件：

• 每块土地应该是一个正方形，且边长是一个正整数。每个正方形的一边应当与道路平行。假设这三块土地的大小分别为 $a \times a$、$b \times b$ 和 $c \times c$。
• 这些正方形的边长之和应该刚好覆盖整条道路，也就是说，$a + b + c = n$。
• 小儿子的土地应该小于二儿子的土地，二儿子的土地应该小于大儿子的土地，也就是说，$a < b < c$。
• 所有区域的总面积 $a^2 + b^2 + c^2$ 应该尽量最小。

给定道路的长度 $n$，你需要求出分配给国王三个儿子的土地的边长。

输入格式

输入一个整数 $n$（$6 \leq n \leq 10^9$）。

输出格式

输出三个数 $a,b,c$。如果有多个最优解，可以输出任意一个。

6

1 2 3

提示

样例解释

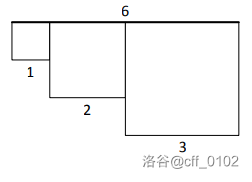
数据范围