题目背景

翻译自 ROIR 2017 D1T4。

题目描述

有一个关于开发邻近星系行星的项目。为了开采矿产资源，计划将几批机器人送往该行星。

该行星的开采区域是一个大小为 $w \times h$ 的矩形网格区域，区域内的单元格坐标范围从 $(1, 1)$ 到 $(w, h)$。在某些单元格中设有基地，可以将机器人按批次运送到那里。整个区域共设有 $s$ 个基地，第 $i$ 个基地位于坐标 $(x_i, y_i)$ 处。

每批机器人有三个重要参数：第 $j$ 批机器人将送往基地 $b_j$，包含 $n_j$ 个机器人，并且每个机器人具有移动能力 $m_j$。

当机器人批次送到相应基地后，每个机器人都会从基地出发，沿着行星表面移动到某个单元格。如果一个机器人的移动能力为 $m$，它最多可以进行 $m$ 次移动，并且每次可以选择八个相邻的方向进行移动，如下图所示。

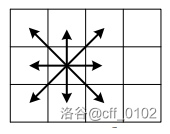
当所有送到的机器人都停止移动后，它们会被激活并开始开采其所在单元格的矿产。在机器人的移动过程中，多个机器人可以同时处于同一个单元格，但是在激活之后，每个单元格内最多只能容纳 $q$ 个机器人。

项目团队得到了 $t$ 批机器人的信息，这些机器人可以按顺序送往行星。然而，考虑到它们的移动限制，如果将所有机器人全部送上去，可能最终无法满足每个单元格最多只有 $q$ 个机器人的要求。因此，项目团队需要选择前 $k$ 批机器人（$0 \leq k \leq t$），将它们完全送到相应的基地。如果 $k < t$，则还可以从第 $k+1$ 批机器人中额外选择 $z$ 个机器人（$0 \leq z < n_{k+1}$）。团队需要求出 $k$ 的最大值，并在这个前提下最大化 $z$（若 $k=t$，则 $z=0$）。

输入格式

第一行输入四个整数 $w, h, s, q$（$ 1 \leq w, h \leq 10^5, 1 \leq s \leq 4, 1 \leq q \leq 100 $）。

接下来 $s$ 行每行包含两个整数 $x_i, y_i$，表示基地的位置（$1 \leq x_i \leq w, 1 \leq y_i \leq h$）。

接下来一行包含一个整数 $t$，表示机器人批次的数量（$1 \leq t \leq 100$）。

接下来的 $t$ 行描述每个机器人批次，每行包含三个整数：$b_j, n_j, m_j$（$ 1 \leq b_j \leq s, 1 \leq n_j \leq w \cdot h \cdot q, 0 \leq m_j < \max(w, h) $）。

输出格式

输出两个整数 $k$ 和 $z$，意义见题目描述。

4 3 2 1
1 1
3 2
3
1 4 1
2 9 1
1 12 2

1 7

提示

样例解释

在样例中，输入了以下信息：

• 区域的大小是 $4 \times 3$，有两个基地，且每个单元格最多容纳 $1$ 个机器人。
• 第一个基地位于坐标 $(1, 1)$，第二个基地位于坐标 $(3, 2)$。
• 总共有 $3$ 批机器人要送往该地区。
  • 第 $1$ 批机器人送往第 $1$ 个基地，包含 $4$ 个机器人，每个机器人的最大移动能力为 $1$。
  • 第 $2$ 批机器人送往第 $2$ 个基地，包含 $9$ 个机器人，每个机器人的最大移动能力为 $1$。
  • 第 $3$ 批机器人送往第 $1$ 个基地，包含 $12$ 个机器人，每个机器人的最大移动能力为 $2$。

经过合理安排，可以让第一批机器人完全送达，并额外选择第二批中的 $7$ 个机器人。最终，第一批和第二批的机器人能够成功安置在网格区域内，使得每个单元格内最多有 $1$ 个机器人：

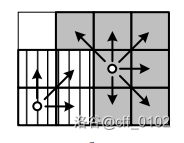
因此，答案是 $k = 1 , z = 7$。

数据范围