luogu#P11489. [BalticOI 2023] Astronomer
[BalticOI 2023] Astronomer
题目描述
给定平面上 个整点,一个正整数 和非负整数 ,在所有至少覆盖了 个点的圆中,设其半径为 ,圆心离原点(即 )距离为 ,试求出 的最小值。
本题中的距离为欧几里得距离。
输入格式
第一行四个非负整数 。
接下来 行,第 行两个整数 表示第 个点的坐标。
输出格式
一行一个实数表示答案。若你的输出和标准答案的相对误差或绝对误差不超过 (在部分子任务中, 的值有变化),你的输出将被判定为正确。
2 3 1000 500
0 0
2 0
3 1
1000.0
2 3 500 3000
0 0
2 0
3 1
3387.277541898787
2 3 250 750
0 0
2 0
3 1
1000.0
2 3 0 500
0 0
2 0
3 1
353.5533905932738
3 4 0 10
0 0
10 0
5 10
5 5
50.0
提示
【样例解释】
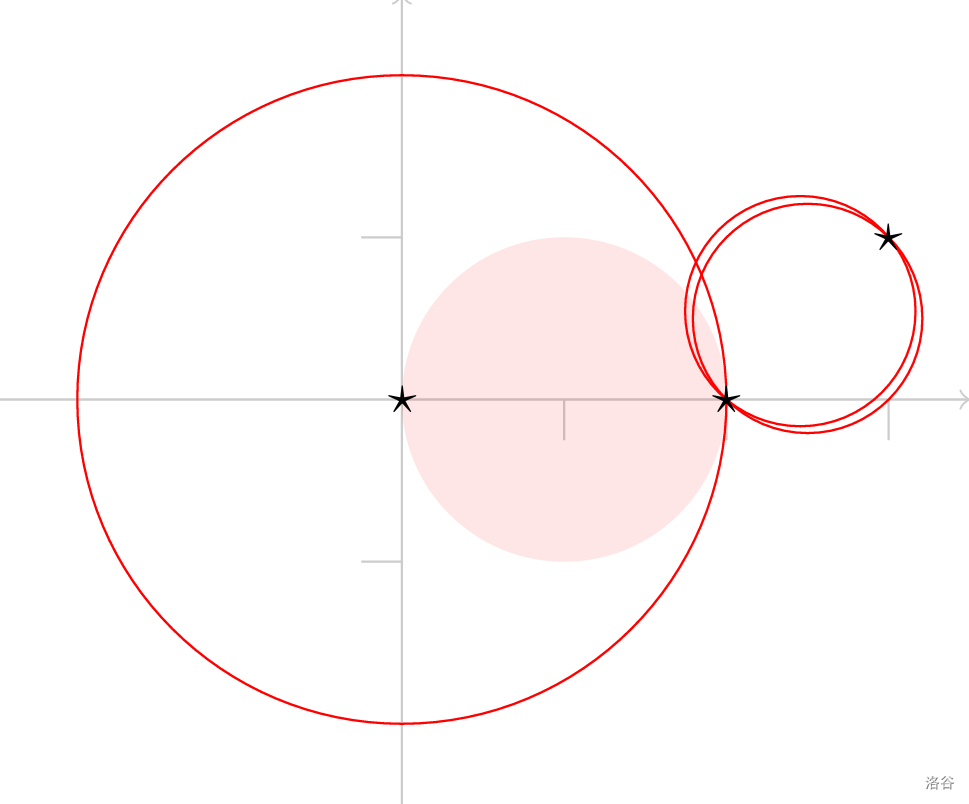
如图,样例 #3 中,最优方案是选择以 为圆心而半径为 的圆(图中粉色实心圆),代价为 。
图中的其它三个圆展示了样例 #1、样例 #2,样例 #4 的最优方案。
【数据范围】
对于 的数据,,,。
| 子任务编号 | 分值 | 特殊限制 |
|---|---|---|
| 且 | ||
| 无特殊限制 |
