题目描述

有 $n$ 名选手，编号分别为 $1, 2, \dots, n$。编号为 $i$ 的选手的实力值为 $i$。所有选手分为红、蓝两队，其中编号为 $i$ 的选手所在的队伍用字符 $s_i$ 描述。$s_i$ 为 R 表示他在红队，$s_i$ 为 B 表示他在蓝队。

现在将所有选手排成一个环，每一对相邻且不属于同一队的选手会进行一场比赛，实力值较大的选手获胜，他所在的队伍的得分增加一。

然而，蓝队的选手勾结了裁判，如果一场比赛中红队选手获胜，且他在蓝队选手的顺时针方向上，则这场比赛不计入得分。

现在你想知道，对于每个 $k = -n, \dots, -1, 0, 1, \dots, n$，有多少种将选手排列的方法，使得红队得分恰好比蓝队得分大 $k$。两种方案不同，当且仅当存在某个选手，使得他顺时针方向的下一个选手在两个方案中不同。

由于答案很大，你只需要输出答案对 $998,244,353$ 取模后的值。

输入格式

从标准输入读入数据。

第一行包含一个整数 $n$，表示选手个数。

第二行包含一个长度为 $n$ 的字符串 $s_1s_2 \dots s_n$，表示每个选手所属的队伍。

输出格式

输出到标准输出。

输出一行 $2n + 1$ 个整数，分别表示 $k = -n, \dots, 0, \dots, n$ 的方案数对 $998,244,353$ 取模后的值。

3
BRB

0 0 1 1 0 0 0

5
RBBRR

0 0 0 0 8 8 8 0 0 0 0

见题目目录下的 3.in 与 3.ans。

见题目目录下的 3.in 与 3.ans。

提示

【样例 1 解释】

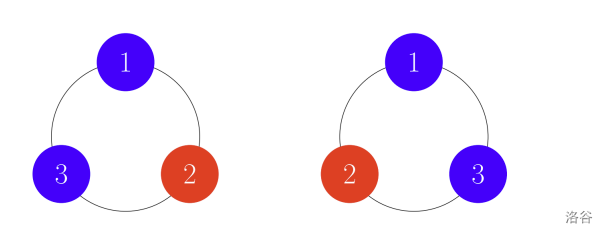
如图所示，共有两种排列的方法。

第一种排列中，选手 $1$ 与 $2$ 之间的比赛虽然选手 $2$ 获胜，但他属于红队，且在选手 $1$ 顺时针方向，故这场比赛不计入得分。而选手 $2$ 和 $3$ 之间的比赛蓝方获胜。因此红队得分为 $0$，蓝队得分为 $1$。

第二种排列中，共进行两场比赛，且均计入得分。红队得分与蓝队得分均为 $1$。

【子任务】

对于所有数据，满足 $3 \leq n \leq 3000$，$s$ 为由 B 和 R 构成的字符串。