题目背景

“只要你心里的念是真的，只要你心里的念是诚的，高山大海都会给你让路。”——《平原上的摩西》

提交时，不要 #include "plain.h"。 将以下的代码粘贴到文件头。

#include <tuple>
#include <utility>
bool query(int x, int y);
std::tuple<long long, int, long long, int> Find(int task_id, int V, int limit);

题目描述

这是一道交互题。

在二维平面上有一条未知的、不与 $y$ 轴平行的直线 $L$。设 $L(x_0)$ 表示直线 $L$ 与 $x = x_0$ 的交点纵坐标。

给定值域 $V$，$L$ 额外满足以下性质：

• 对于任意整数 $0 \le x, y \le V$，$L(x)\neq y$；
• $0 \le L(0), L(V ) \le V$。

此时 $L$ 将 $S = \{0, 1, 2, \cdots , V \} × \{0, 1, 2, \cdots , V \}$ 分割成两个点集 $S_L = \{(x, y) \in S \vert L(x) > y\}$ 和 $\overline{S_L} = \{(x, y) \in S | L(x) < y\}$，且它们都不是空集。

你可以向交互库询问至多 $\mathrm{limit}$ 次询问。每次询问给出整数 $0 \le x, y \le V$ ，你可以得到 $(x, y)$ 属于 $S_L$ 还是 $\overline{S_L}$。

你需要找到直线 $L'$，其不经过 $S$ 中任何一个点，且 $L'$ 和 $L$ 将 $S$ 划分为同样的两个点集。形式化地，$L'$ 需要满足 $\forall(x, y) \in S_L, L'(x) > y$ 且 $\forall(x, y) \in \overline{S_L}, L'(x) < y$。

实现细节

在洛谷上提交时，请确保你的程序开头没有 #include "plain.h"。

你不需要也不应该实现主函数。你需要实现以下函数：

• std::tuple<long long, int, long long, int> Find(int task_id, int V, int limit);
  • 其中 task_id 表示子任务编号，V 表示值域，limit 表示最大询问次数。
  • 你需要返回四元组 $(k_u, k_v, b_u, b_v)$ 表示你给出的直线 $L'$ 的解析式为 $y = \frac{k_u}{k_v} x + \frac{b_u}{b_v}$。
  • 你需要保证 $k_u$ 与 $b_u$ 在 long long 范围内，$k_v$ 与 $b_v$ 在 int 范围内，且 $k_v,b_v> 0$。你不需要保证给出的分数是既约分数。可以证明在本题的数据范围下，总是存在这样的 $(k_u, k_v, b_u, b_v)$ 满足条件。
  • 在最终测试时，交互库将会调用 $T \le 10^4$ 次 Find 函数。

你可以使用 std::make_tuple(a,b,c,d) 来将 $a,b,c,d$ 打包成一个 tuple。

你可以调用如下函数进行一次询问：

• bool query(int x,int y);
  • 你需要保证 $0 \le x, y \le V$ ，在单组测试数据内该函数的调用次数不超过 $\mathrm{limit}$。
  • 当 $(x, y) \in S_L$ 时，函数返回 true，否则返回 false。

保证在满足题目条件和数据范围的情况下，最终测试时交互库的运行时间不会超过 $\text{200 ms}$，运行空间不会超过 $\text{64 MiB}$。

交互库不是自适应的，即 $L$ 是固定的，不会随着交互过程改变。

测试程序方式

试题目录下的 grader.cpp 是我们提供的交互库参考实现。最终测试的交互库与样例交互库有一定不同，故你的实现不应该依赖样例交互库实现。

你需要在本题目录下使用如下命令编译得到可执行程序：

g++ plain.cpp grader.cpp ‐o plain ‐O2 ‐‐std=c++14 ‐lm

对于编译得到的可执行程序：

• 可执行文件将从标准输入读入以下格式的数据：
  • 第一行三个整数 $\mathrm{task\_id}, T, \mathrm{limit}$，分别表示子任务编号，测试数据组数和每组测试数据的询问次数上限。接下来依次输入每组测试数据。
  • 对于每组测试数据输入一行五个整数 $V, k_u, k_v, b_u, b_v$，其中 V 表示值域，$k_u, k_v, b_u, b_v$ 表示直线 L 的解析式为 $y = \frac{k_u}{k_v} x + \frac{b_u}{b_v}$。
  • 你需要保证 $b_u$ 在 long long 范围内，$k_u, k_v, b_v$ 在 int 范围内，且 $k_v, b_v > 0$。

对于所有测试数据，保证存在这样的 $(k_u, k_v, b_u, b_v)$ 满足题目条件。

• 读入完成之后，交互库将会调用 $T$ 次 Find 函数。
• 若每一组测试数据中你都在给定的询问次数内求出了正确的直线，交互库将在标准输出流输出两行，第一行一个字符串 $\texttt{Correct.}$，第二行一个整数，表示 $T$ 组测试数据中 query 调用次数的最大值。否则交互库会输出对应错误信息，并立即停止程序。

输入格式

见【测试程序方式】。

输出格式

见【测试程序方式】。

0 3 20
4 5 11 11 6
4 ‐11 15 17 5
4 2 15 4 5

Correct.
8

提示

【样例 $1$ 解释】

$\mathrm{task\_id} = 0$ 表示该组数据为样例。

下面三张图依次展示了三组数据对应的函数图像。

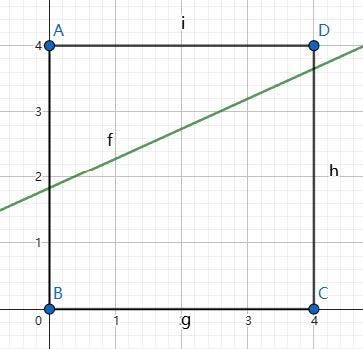
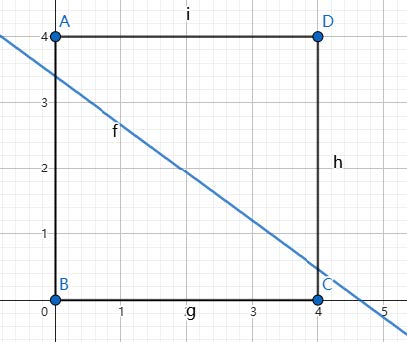
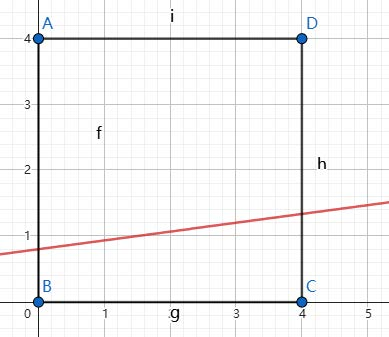
子任务

对于所有测试数据，$2 \le V \le 10^9$，$1 \le T \le 10^4$，$100 \le \mathrm{limit} \le 3, 666$。

---

子任务编号	分值	$V$	$T$	$\mathrm{limit}$	特殊性质
1	$20$	$\le 10^2$	$\le 10$	$=110$	无
2		$\le 10^9$	$\le 10^3$		A
3	$10$	$\le 10^5$	$\le 10$	$=1,111$	无
4	$15$	$\le 10^9$	$\le 500$	$=3,666$
5	$20$	$\le 10^5$	$\le 10$	$=10^2$
6	$10$	$\le 10^9$		$=180$
7	$15$		$\le 10^4$

特殊性质 A：保证直线 $L$ 是由 $y = \frac{a}{b}x$ 向上平移至多 $\frac{1}{2b}$ 得到的，其中 $0 < b \le V$。

评分方式

本题首先会受到和传统题相同的限制。例如编译错误会导致整道题目得 $0$ 分，运行时错误、超过时间限制、超过空间限制都会导致相应测试点得 $0$ 分。选手只能在程序中访问自己定义的和交互库给出的变量或数据，及其相应的内存空间。尝试访问其他位置空间将可能导致编译错误或运行错误。

当你在每次 Find 调用中，程序调用的 query 函数次数不超过 limit，且返回的 $L'$ 均满足题目描述中的条件，即通过该测试点，否则该测试点不通过。只有你通过一个子任务的所有测试点时，才能获得该子任务的所有分数。

选手不应通过非法方式获取交互库的内部信息，如试图与标准输入、输出流进行交互。此类行为将被视为作弊。