luogu#P11364. [NOIP2024] 树上查询
[NOIP2024] 树上查询
题目描述
有一天小 S 和她的朋友小 N 一起研究一棵包含了 个结点的树。
这是一棵有根树,根结点编号为 ,每个结点 的深度 定义为 到 的简单路径上的结点数量。
除此之外,再定义 为编号在 中所有结点的最近公共祖先,即 的公共祖先结点中深度最大的结点。
小 N 对这棵树提出了 个询问。在每个询问中,小 N 都会给出三个参数 ,表示他想知道 中任意长度大于等于 的连续子区间的最近公共祖先深度的最大值,即
$$\max_{l\le l'\le r'\le r \land r'-l'+1\ge k}\text{dep}_ {\text{LCA*}(l', r')} $$你的任务是帮助小 S 来回答这些询问。
输入格式
输入的第一行包含一个正整数 ,表示树的结点数。
接下来 行,每行包含两个正整数 ,表示存在一条从结点 到结点 的边。
第 行包含一个正整数 ,表示询问的数量。
接下来 行,每行包含三个正整数 ,描述了一次询问。
输出格式
对于每次询问输出一行,包含一个整数,表示对应的答案。
6
5 6
6 1
6 2
2 3
2 4
3
2 5 2
1 4 1
1 6 3
3
4
3
提示
【样例 1 解释】
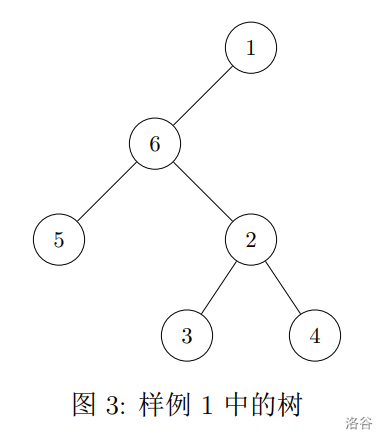
-
对于第一组询问,$\text{LCA*}(2, 3) = 2, \text{LCA*}(3, 4) = 2, \text{LCA*}(4, 5) = 6$, 的深度为 , 的深度为 ,因此答案为 。
-
对于第二组询问,答案为 四个结点的最大深度,因此答案为 。
-
对于第三组询问,$\text{LCA*}(1, 3) = 1, \text{LCA*}(2, 4) = 2, \text{LCA*}(3, 5) = 6, \text{LCA*}(4, 6) = 6$,依旧是 的深度最大,因此答案为 。
【样例 2】
见附件的 query/query2.in 与 query/query2.ans。
该样例满足 。
【样例 3】
见附件的 query/query3.in 与 query/query3.ans。
该样例满足 且树符合链的形态。
【样例 4】
见附件的 query/query4.in 与 query/query4.ans。
该样例满足 。
【数据范围】
对于所有的测试数据,保证:$1 ≤ n, q ≤ 5 × 10^5 , 1 ≤ l ≤ r ≤ n, 1 ≤ k ≤ r - l + 1$
| 测试点编号 | 特殊限制 | |
|---|---|---|
| 无 | ||
| 满足性质 A | ||
| 满足性质 B | ||
| 无 | ||
性质 A:保证输入的树符合链的形态,且根结点的度数为 。
性质 B:对于每个询问保证 。
