题目描述

你的公司要在 $N\times M$ 的网格图上建造办公室。如图所示，网格图上有横着和竖着的边，其边权均为 $1$。

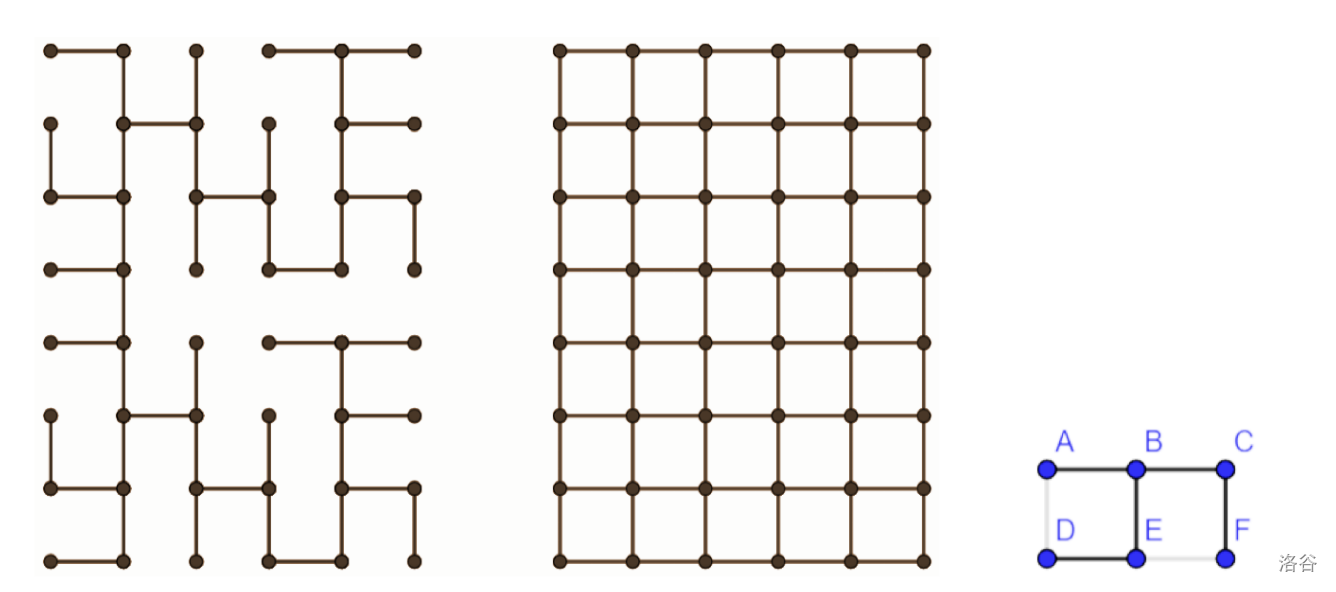
在白天，所有道路都是可以走的。在晚上，只有 $N\times M-1$ 条边有照明且可以走。

你喜欢巡视办公室。每天，你都会以一个顺序从一个办公室开始，经过可用的边遍历每个办公室一次，最后回到起点。你希望选择网格图上一个点的子集 $S$，满足其在白天和晚上进行巡视所需走过的最短路径长度相等。

你希望计算三种条件下，可能的 $S$ 的数量对 $10^9+7$ 取模的值：

1. $|S|\geq 2$。
2. $|S|=2$。
3. $|S|=3$。

输入格式

第一行输入三个整数 $N,M,T$，其中 $T$ 代表你需要计算的问题编号。

接下来 $N$ 行，每行输入一个长度为 $M$ 的字符串 $A_{i,j}$。

• $A_{i,j}\in\{\texttt{1},\texttt{3}\}$ 代表 $(i,j)$ 有连向 $(i-1,j)$ 的边。
• $A_{i,j}\in\{\texttt{2},\texttt{3}\}$ 代表 $(i,j)$ 有连向 $(i,j-1)$ 的边。

保证输入的是一棵树。

输出格式

输出一个整数，代表答案对 $10^9+7$ 取模的值。

2 3 2
022
031

12

2 3 3
022
031

10

2 3 1
022
031

25

提示

【样例解释】

如上方示意图所示。

以下为 $|S|=2$ 的方案：$\{A,B\}$，$\{A,C\}$，$\{A,E\}$，$\{A,F\}$，$\{B,C\}$，$\{B,D\}$，$\{B,E\}$，$\{B,F\}$，$\{C,D\}$，$\{C,E\}$，$\{C,F\}$，$\{D,E\}$。

以下为 $|S|=3$ 的方案：$\{A,B,C\}$，$\{A,B,E\}$，$\{A,B,F\}$，$\{A,C,E\}$，$\{A,C,F\}$，$\{B,C,D\}$，$\{B,C,E\}$，$\{B,C,F\}$，$\{B,D,E\}$，$\{C,D,E\}$。

以下为 $|S|=4$ 的方案：$\{A,B,C,E\}$，$\{A,B,C,F\}$，$\{B,C,D,E\}$。

【数据范围】

本题采用捆绑测试。

• Subtask 1（4 pts）：$N,M\leq 2$。
• Subtask 2（5 pts）：$N=1$。
• Subtask 3（9 pts）：$T=2$，$N,M\leq 50$。
• Subtask 4（11 pts）：$T=2$。
• Subtask 5（9 pts）：$T=3$，$N,M\leq 20$。
• Subtask 6（13 pts）：$T=3$。
• Subtask 7（14 pts）：$T=1$，$N,M\leq 4$。
• Subtask 8（10 pts）：$T=1$，$N,M\leq 50$。
• Subtask 9（9 pts）：$T=1$，$A_{i,j}\neq \texttt{3}$。
• Subtask 10（16 pts）：$T=1$。

对于 $100\%$ 的数据，保证 $1\leq T\leq 3$，$1\leq N,M\leq 10^3$，$A_{i,j}\in\{\texttt{0},\texttt{1},\texttt{2},\texttt{3}\}$。