题目背景
翻译自 ROI 2024 D1T4。
拉马赞决定从事一个重要的业务——种植白菜。种植白菜的场地是一个无限大的网格场地。每个网格单元可以种植一个白菜。拉马赞只种植了场地的一部分。他计划利用其中的几个矩形区域,这些矩形可能会相交。如果一个网格单元位于至少一个矩形内,则该单元被认为种植了白菜。
具体地,拉马赞选择了 n 个矩形区域,矩形的坐标为 (xLi,yLi,xRi,yRi) (其中 xLi≤xRi,yLi≤yRi,1≤i≤n)。如果存在至少一个矩形 i (1≤i≤n),使得 xLi≤x≤xRi 且 yLi≤y≤yRi,则认为网格单元 (x,y) 被种植了白菜。

拉马赞曾经是一个程序员(并且还是一个获奖者),因此他决定使用人工智能机器人定期处理种植。一个机器人可以服务于任意的水平区域 $(x_{\text{robot}_1}, x_{\text{robot}_2}, y_{\text{robot}})$,即所有满足 xrobot1≤x≤xrobot2 且 y=yrobot 的网格单元 (x,y)。
重要的是,机器人只能在种植的区域内移动。他明白,为了最小化机器人的数量,需要使用那些不能进一步扩展的水平区域。如果满足以下条件,拉马赞将使用机器人在网格单元 $(x_{\text{robot}_1}, x_{\text{robot}_2}, y_{\text{robot}})$ 上工作:
- 所有满足 xrobot1≤x≤xrobot2 且 y=yrobot 的网格单元 (x,y) 都属于种植区域;
- 网格单元 (xrobot1−1,yrobot) 不属于种植区域;
- 网格单元 (xrobot2+1,yrobot) 不属于种植区域。
题目描述
你需要收集有关机器人在种植区域工作的统计信息。如果存在一个机器人恰好在网格段 (x1,x2,y) 上工作,我们说 (x1,x2) 在行 y 上被服务。具体地,你需要:
- 找出所有在某一行中被服务的 (x1,x2) 对。
- 对于每一对这样的 (x1,x2),找出它被服务的行数。
- 对于每一对这样的 (x1,x2),找出它被服务的最大连续行数。换句话说,找出最大值 k,使得存在一个长度为 k 的连续行区间 [y1,y2](其中 y2−y1+1=k),使得在任意行 y1≤y≤y2 中,该对 (x1,x2) 都被服务。
输入格式
输入包含多组数据。第一行给出一个整数 t(1≤t≤200000),表示测试数据的组数。
每组数据的第一行给出一个整数 n(1≤n≤200000),表示矩形区域的数量。
接下来的 n 行中,每行包含四个整数 xLi,yLi,xRi,yRi(1≤xLi≤xRi≤109,1≤yLi≤yRi≤109),表示一个矩形区域。
令 N 表示所有数据集中的 n 总和,保证 N≤200000。
输出格式
对于每组数据,首先输出一个整数 p(p≥1),表示在某一行中被服务的 (x1,x2) 对的数量。接下来 p 行中,每行输出四个整数 x1,x2,cnt,k(1≤x1≤x2≤109,0≤cnt,k≤109)。其中,cnt 是该对 (x1,x2) 被服务的行数,k 是它被服务的最大连续行数。
每一对 (x1,x2) 必须是不同的。每一对在某一行中被服务的 (x1,x2) 对,必须输出且只能输出一次。输出顺序可以是任意的。
4
2
2 2 3 3
3 3 4 4
2
2 1 2 3
1 2 3 2
4
2 2 4 5
3 4 9 7
2 9 9 10
7 1 9 7
7
2 1 2 9
5 1 6 8
4 5 7 6
1 8 4 10
1 6 3 6
1 2 7 3
4 1 7 1
3
2 3 1 1
2 4 1 1
3 4 1 1
2
1 3 1 1
2 2 2 1
4
2 4 2 2
2 9 4 2
3 9 2 2
7 9 3 3
6
1 4 2 2
1 6 1 1
1 7 3 2
2 2 4 2
4 7 2 1
5 6 2 1
提示
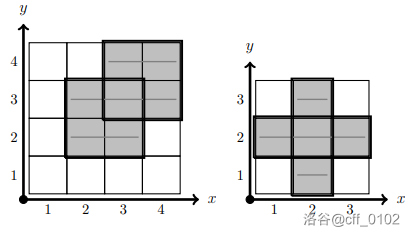
在第一组数据中,机器人在以下区段进行服务:(2,3,2),(2,4,3) 和 (3,4,4)。因此,对 (2,3),(2,4) 和 (3,4) 在某一行中得到服务,并且每对都只在一行中被服务。
在第二组数据中,机器人在以下区段进行服务:(2,2,1),(2,4,2) 和 (2,2,3)。因此,对 (2,2) 和 (2,4) 在某一行中得到服务。对 (2,2) 在第 1 行和第 3 行中得到服务,而对 (2,4) 在第 2 行中被服务。
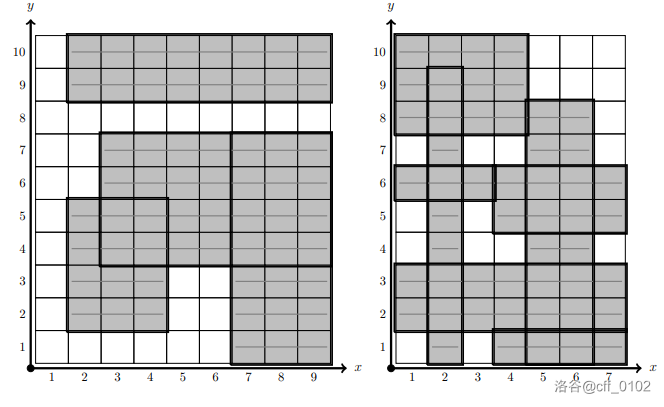
下面是第三和第四组数据的图片。
- 如果你的程序错误地找出了在某一行中被服务的对 (x1,x2) 的集合,该测试点将获得零分。
- 如果你的程序:
- 能够正确找出该集合,但不是所有的 cnt 都正确,该测试点将获得 50% 的分数。
- 能够正确找出该集合和所有 cnt,但不是所有的 k 都正确,该测试点将获得 75% 的分数。
- 能够正确找出该集合、所有 cnt 和所有 k,该测试点将获得 100% 的分数。
请注意,如果你想获得获得部分分,仍需为每对配对 (x1,x2) 输出一些 cnt 和 k 值,但不必全部正确。



