loj#P6579. 「ICPC World Finals 2019」事后检查
「ICPC World Finals 2019」事后检查
题目描述
你们大学的桌游俱乐部最近举办了跳棋锦标赛,你在比赛中担任记录游戏过程的职务。不幸的是,在你回家的过程中,你没有拿稳游戏记录,它们全都掉入了水坑。这一灾难性的事件使得你记下的大部分记录都变得不可阅读了。现在你只剩下几局游戏中途的几次移动了,但你需要把这几局游戏的全程恢复出来。如果你没能恢复回来,你以后就只能去记录井字棋的游戏过程了。
跳棋是一个著名的桌游,它的游戏规则也很简单。它由两名玩家各执黑白两种棋子在一个 的正方形区域组成的黑色跳棋板上轮流游玩。其中,每种棋有两种形态:普通人(普通形态)和皇后(升级形态)。在每一回合中,玩家都要选择一个棋子并进行如下之一的移动:
- 如图 (a) 所示,将一个棋子斜着移动到一个没有棋子的相邻区域,这种移动称作「简单移动」。但是,如果这个棋子的形态是普通人,它只能沿着两种方向移动(黑棋只能向下移动,白棋只能向上移动);如果这个棋子的形态是皇后,则它可以沿着四种方向移动。
- 沿斜线方向跳过对方的棋子,然后到达一个没有棋子的格子,然后吃掉所跳过的那颗棋子。如果这个棋子的形态是普通人,它只能沿着上述两种方向移动;如果这个棋子的形态是皇后,则它可以沿着四种方向移动。只要还能继续按本方法进行移动,玩家在一个回合内可以多次执行这个操作。一次或多次执行本移动操作的操作序列叫做「跳跃移动」。图 (b) 展示了一个由三次移动组成的跳跃移动。
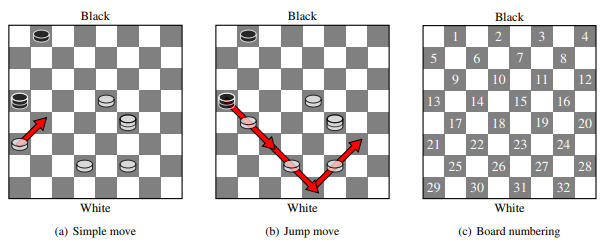
图 (c) 是在输入中用到的编号。
在本游戏中,跳跃移动是强制行为。如果在一个玩家的回合一开始有可以进行的跳跃移动,他必须进行此移动,直至没有可以进行的移动。如果有多种可行的操作,他们可以自由选择将哪颗棋子跳到哪。在图 (b) 中,黑棋没有其他移动的方案。
如果一个普通人形态的棋子到达了离它最远的那一行(即,普通人形态的黑棋到达了最下面的一行,或者普通人形态的白棋到达了最上面的一行),它将被从桌面上拿走,并换成同色的皇后棋子(这一操作叫做「升级」),然后回合结束。皇后不能被升级,它将在同一回合内被当做一个新皇后往后跳回去。
给出一系列操作,找出一个起始状态使得以该状态为初始状态时序列中的操作可以合法地依次进行。在这个起始状态中,不能有黑色的普通人形态的棋子在棋盘底部,也不能有白色的普通人形态棋子在棋盘顶部,这是因为这些棋子处在这些位置时已经升级成了皇后了。你需要做的只是保证满足以上条件而不用考虑该状态在现实的游戏中是否可行。
输入格式
第一行包括一个字符 和一个整数 。其中 表示先走棋的玩家, 要么为 B,要么为 W,分别表示黑棋玩家先走和白棋玩家先走, 为列表内的操作数。接下来 行,每行以标准跳棋记录格式描述一个移动。
黑色的格子被编号为 ,如图 (c) 所示。从编号为 的格子到编号为 的格子的简单移动被描述为 a-b,而从编号为 的格子开始,依次到达 的跳跃移动记做 。
输入数据保证有解。
输出格式
输出两个并排的棋盘,以空格分隔,左边的那个表示移动前的棋子位置,右边的表示移动后的棋子位置。用 - 表示白色的格子,用 . 表示空着的黑色格子,用 b 和 w 分别表示黑色和白色的普通人形态的棋子,用 B 和 W 分别表示黑色和白色的皇后形态的棋子。
如果多解,输出任意一个。
W 3
21-17
13x22x31x24
19x28
-b-.-.-. -b-.-.-.
.-.-.-.- .-.-.-.-
-.-.-.-. -.-.-.-.
B-.-w-.- .-.-w-.-
-.-.-W-. -.-.-.-.
w-.-.-.- .-.-.-.-
-.-w-w-. -.-.-.-W
.-.-.-.- .-.-.-.-
B 5
2-7
9x2
32-27
2x11x18
5-9
-.-b-.-W -.-.-.-W
b-b-.-.- .-.-.-.-
-w-.-.-. -b-.-.-.
B-w-b-.- B-w-.-.-
-.-.-.-. -.-W-.-.
.-.-.-.- .-.-.-.-
-.-.-.-. -.-.-B-.
.-.-.-B- .-.-.-.-
数据范围与提示
对于 的数据,。
