题目描述

一个经典的问题是用一个国际象棋的骑士走遍 $8 \times 8$ 的棋盘，其中骑士只能通过沿一个方向跳动一个方块并沿对角线方向跳动一个方块来移动。骑士必须不重复地走完棋盘的每个方块并回到起始点。因为方案很多，且棋盘的大小固定，所以对人类来说这是可以解决的。

但你有一台电脑，还懂得编程！所以你需要解决一个更难的问题：棋盘大小为 $m \times n$ 且骑士的路径不能自交。如果把骑士路径上的格子中心点相连的话，这些点必须形成一个简单多边形；也就是说除了相邻的线段在顶点上接触以外，没有任何两个线段相交或接触。这个限制条件啊导致不重复地经过每个格子变得不可能，所以你只要最大化骑士经过的格子数量。我们仍然要求骑士必须回到出发点。下图显示了第一个样例输入（$6 \times 6$ 棋盘）对应的最优解。

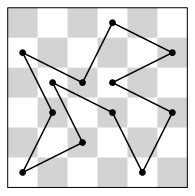
输入格式

输入共一行两个数 $m\ (1 \le m \le 8)$ 和 $n\ (1 \le n \le 10^{15})$，表示矩形棋盘的大小。

输出格式

输出骑士在路径不自交的情况下能在棋盘上走过的最多方格数。如果没有这样的路径，输出 $0$。

6 6

12

8 3

6

7 20

80

2 6

0

数据范围与提示

在不侵犯原题版权的情况下，本题面中文翻译基于知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议发布，注明出处时需指向本题链接。