题目描述

本题译自 eJOI2022 Problem B. Where Is the Root?

这是一道交互题。

给定一个有 $n$ 个节点的树。树是满足任意两不同点之间恰好有一条简单路径的图。同时保证至少有一个节点，这个节点与至少三个节点直接有边相连。其中一个节点是根，你的任务是找到它。为了完成这个任务，你允许问如下格式的问题：

• 对于给定的点集 $a_1,a_2,\ldots,a_m$，检查它们的最近公共祖先是否在集合中。

如果所有 $S$ 中的点到根的路径都经过 $v$，那么就称节点 $v$ 是点集 $S$ 的公共祖先。点集 $S$ 的最近公共祖先（LCA）就是点集 $S$ 的公共祖先中距离根最远的那个。

交互方式

通过读入一个整数 $n\ (4\le n\le 500)$ 开始整个交互过程，$n$ 表示节点个数。

接着读入 $n-1$ 行。第 $i$ 行包含两个整数 $a_i,b_i\ (1\le a_i,b_i\le n)$，表示树上 $a_i$ 与 $b_i$ 两点之间有一条边。

保证这 $n-1$ 条边可以形成一棵树，并且至少有一个节点，这个节点与至少三个节点直接有边相连。

如果要询问的话，首先输出 ?，然后输出一个整数 $m$，然后输出 $m$ 个互不相同的整数 $a_1,a_2,\ldots,a_m\ (1\le m\le n,1\le a_i\le n)$，表示你想要检查这些节点的 LCA 是否在其中。

作为回答，如果它们的 LCA 是 $a_1,a_2,\ldots,a_m$ 中的一个的话，交互器将会输出 YES，否则输出 NO。

你可以最多问 $1000$ 个问题，但是根据你问的问题个数会得到不同的得分。输出答案不算一次询问。请查看「评分」一节了解细节。

当你确定了根的时候，先输出 !，然后输出一个整数 $v\ (1\le v\le n)$，表示根。然后终止你的程序。

在输出一次查询后，不要忘记输出换行并刷新输出缓冲区。为了实现这点，使用：

• fflush(stdout) 或者 cout.flush()，对于 C++ 语言；
• stdout.flush()，对于 Python 语言。

保证对于每个测试点，树的根是在交互过程之前确定的。换句话说，交互器是非自适应性的。

样例交互

Input:
7
4 1
1 2
4 3
3 5
3 6
4 7
Output:
? 2 5 6
Input:
NO
Output:
? 3 6 3 5
Input:
YES
Output:
? 2 1 7
Input:
NO
Output:
? 2 4 6
Input:
YES
Output:
! 4

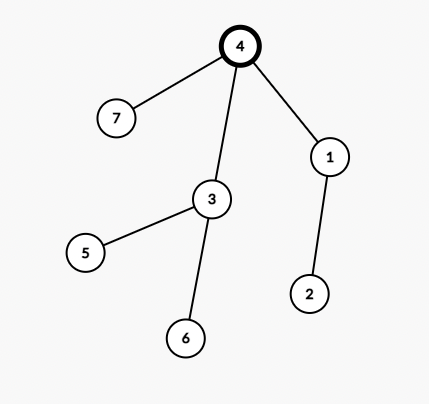
隐藏的根是节点 $4$。

在第一个询问中，$5$ 和 $6$ 的 LCA 是 $3$，不在 $5$ 和 $6$ 中，因此输出 NO。

第二个询问中，$3,5,6$ 的 LCA 是 $3$，所以输出 YES。

第三个询问中，$1$ 和 $7$ 的 LCA 是 $4$，所以输出 NO。

第四个询问中，$4$ 和 $6$ 的 LCA 是 $4$，所以输出 YES。

在此之后，我们可以猜到根是节点 $4$，并且这是正确答案。

评分

详细子任务附加限制及分值如下表所示。

子任务编号	附加限制	分值
$1$	$n\le 9$	$7$
$2$	$n\le 30$	$10$
$3$	$n\le 500$	$83$

在第一和第二个子任务中，你可以最多询问 $1000$ 次。

在第三个子任务中，令 $k$ 是你在任何测试数据上的最大询问次数。如果 $k\le 9$，你会获得 $83$ 分。否则，你会获得 $\lfloor\max(10,83\cdot(1-\frac{\ln(k-6)}{7}))\rfloor$ 分。

计算第三个子任务得分的 C++ 代码如下：

((k <= 9) ? 83: max(10, int(83 * (1 - log(k - 6.0) / 7))))