loj#P3466. 「COCI 2021.2」Planine
「COCI 2021.2」Planine
Description
Zoran wanders across his Dalmatian homeland to forget his love woes. He came across a mountain of a specific shape, behind which a young maiden is waiting for him. The mountain can be described with alternating low and high points, where is odd. Points at odd indices, except the first and the last point, are called .
Zoran is afraid of the dark. Even the call of love will not give him courage to cross the mountain at night. As usual, the fairies of Velebit come to the rescue.
We model each fairy by a luminous dot at a fixed height . A fairy illuminates the valley if and only if the segment connecting the fairy and the valley does not intersect the interior of the mountain.
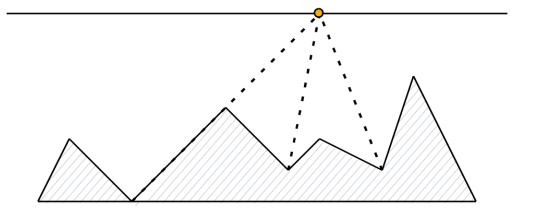 The mountain from the first example, and a fairy illuminating all three valleys.
The mountain from the first example, and a fairy illuminating all three valleys.
What is the least number of fairies which can illuminate all the valleys simulaneously?
Input
The first line contains two integers odd and , the number of points describing the mountain and the height the fairies live at.
The -th of the following lines contains integers and , the coordinates of the -th point of the mountain.
It is guaranteed that , and .
Output
Output the least number of fairies such that all valleys are illuminated.
9 6
0 0
1 2
3 0
6 3
8 1
9 2
11 1
12 4
14 0
1
9 5
-5 2
-4 3
-2 1
0 4
2 2
3 3
4 1
5 2
6 1
2
Scoring
| Subtask | Constraints | Points |
|---|---|---|
| No additional constraints. |
