loj#P2758. 「JOI 2014 Final」年轮蛋糕
「JOI 2014 Final」年轮蛋糕
题目描述
译自 JOI 2014 Final T3「バームクーヘン」
JOI 君马上要和妹妹 JOI 子和 JOI 美一起吃小吃。今天的小吃是他们三个人都很喜欢的年轮蛋糕。
年轮蛋糕是像下图一样呈圆筒形的蛋糕。为了把蛋糕分给三个人,JOI 君必须沿着半径方向切 刀,从而把蛋糕分成三块。然而,由于年轮蛋糕硬得像实木一样,要让刀切进去并不简单。因此,这个年轮蛋糕上事先准备了 个切口,而 JOI 君只能在有切口的位置下刀。切口按顺时针顺序编号为 到 ,对于 ,第 个切口和第 个切口之间部分的大小是 。第 个切口和第 个切口之间部分的大小是 。
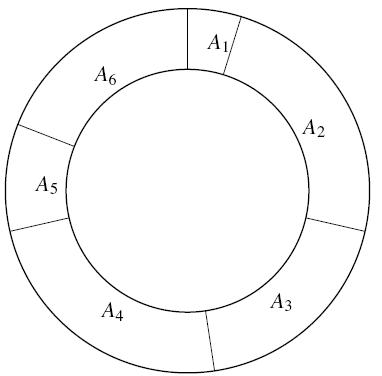
图 1:一个年轮蛋糕的例子,$N=6,A_{1}=1,A_{2}=5,A_{3}=4,A_{4}=5,A_{5}=2,A_{6}=4$
妹控的 JOI 君在把蛋糕切成 块之后,自己选走最小的一块吃掉,把剩下两块分给两个妹妹。而另一方面,JOI 君太喜欢年轮蛋糕了,只要能吃到的时候就会想吃很多很多。试求:JOI 君吃掉的蛋糕的大小至多不超过多少。
给出切口个数 和表示各部分大小的整数 ,请求出把年轮蛋糕切成 块之后最小一块大小的最大值。
输入格式
第 行有一个整数 ,表示年轮蛋糕上有 个切口; 接下来有 行,第 行有一个整数 ,表示第 个切口和第 个切口之间部分(当 时即为第 个和第 个之间部分)的大小。
输出格式
输出一行,一个整数,表示当把年轮蛋糕切成 块之后最小块大小的最大值。
6
1
5
4
5
2
4
6
30
1
34
44
13
30
1
9
3
7
7
20
12
2
44
6
9
44
31
17
20
33
18
48
23
19
31
24
50
43
15
213
数据范围与提示
全部的输入数据满足:
子任务 1( 分)
满足 。
子任务 2( 分)
满足 。
子任务 3( 分)
满足 。
子任务 4( 分)
没有额外限制。
