题目描述

译自 JOI 2015 Final T2「ケーキの切り分け２」

JOI 君和 IOI 酱是双胞胎兄妹。 JOI 君最近闲暇时常常会做甜点。今天 JOI 君也烤了蛋糕吃，IOI 酱立马嗅到了蛋糕的香气于是跑来想分着吃。
蛋糕是圆形的，从蛋糕中某点开始将蛋糕放射状切为 $N$ 块，按逆时针顺序编号为 $1$ 到 $N$ 。切了之后的第 $i$ 块蛋糕的大小为 $A_i$ 。由于切蛋糕的人刀功很不好，所以 $A_i$ 互不相同。

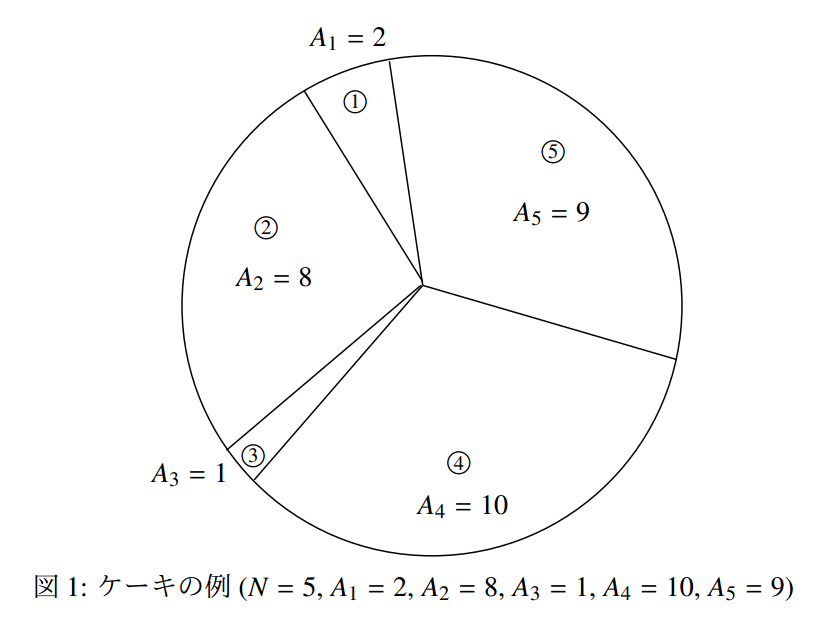
JOI 君和 IOI 酱按照以下的方法分这 $N$ 块蛋糕：

1. 首先 JOI 君从这 $N$ 块蛋糕中任选一块取走；
2. 然后，从 IOI 酱开始， IOI 酱和 JOI 君交替地从剩下的蛋糕中选出一块取走。不过，当且仅当一块蛋糕两旁的蛋糕至少有一块已经被选择，这块蛋糕才能被选择。如果可供选择的蛋糕有多个， IOI 酱会选择最大的一个，而 JOI 君可以任选一个。

JOI 君想让自己所得到的蛋糕大小的合计值最大。

任务

给出蛋糕的块数 $N$ 和这 $N$ 块蛋糕的大小。请编写程序求出 JOI 君得到的蛋糕大小的总和的最大值。

输入格式

第一行为整数 $N$ ，表示蛋糕被切成了 $N$ 块；
接下来 $N$ 行中的第 $i$ 行 $(1 \leq i \leq N)$ 为一个整数 $A_i$ 。表示第 $i$ 块蛋糕的大小。

输出格式

输出一行： JOI 君得到的蛋糕大小的总和的最大值。

5
2
8
1
10
9

18

8
1
10
4
5
6
2
9
3

26

15
182243672
10074562
977552215
122668426
685444213
3784162
463324752
560071245
134465220
21447865
654556327
183481051
20041805
405079805
564327789

3600242976

数据范围与提示

对于所有数据，$1 \leq N \leq 2000,$ $1 \leq A_i \leq 10^9,$ 每个 $A_i$ 都不同。

子任务 1（15 分） $\ \ N \leq 20$。
子任务 2（45 分） $\ \ N \leq 30$。
子任务 3（40 分） 无追加限制。