题目描述

W 教授在 T 大学计算机系里开了一门「数字逻辑」课，主要讲授如何设计逻辑电路。这一天，W 教授布置了一个实验：设计并实现一个 $4$ 端输入、$4$ 端输出的逻辑译码电路。设计这样的电路原本并不困难，但是，教授给出了如下的要求：

1. 只允许使用 $2$ 端输入、$1$ 端输出的门电路作为实现电路的组件，而且可用门电路的种类和数目都已给定；
2. 使用最少数目的门电路。

这两个要求难倒了全系的同学，于是，Q 同学找到了正在参加 CTSC（中国队选拔赛）的你，希望你能帮忙编写一个程序，自动找出符合要求的连接方式。

在数字逻辑中，所有信号都可以看作只有两个值：「高电平」和「低电平」，分别用 $1$ 和 $0$ 来表示。

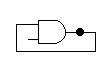
一个门电路元件的特性由其输入/输出功能表唯一给出，所谓功能表，就是输入信号电平与输出信号电平之间的关系表。比如，「与门」的符号和功能表如下图所示：

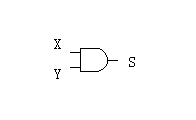
X	Y	S
0	0	0
1
0	1
1		1

上图中，如果「与门」的两个输入端 X 和 Y 都是高电平 $1$，则输出端 S 也是高电平 $1$，否则，输出端 S 是低电平 $0$。

假定，本次实验提供的门电路都具有输入对称性，即交换两个输入端的信号，输出不变。但是，如果门电路的输入端悬空（即没有加输入信号），则输出无意义。

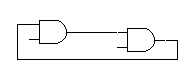
在连接电路的过程中，一个门电路的输出端可以将信号送到其他多个元件的输入端；而门电路的一个输入端则只能接收来自一个输出端的信号。如下图所示：

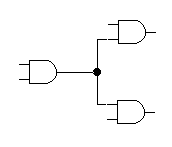
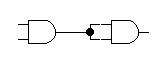
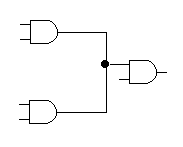
其中，前两个连接方式是允许的，最后一个是不允许的。

另外，规定信号必须单向传输，即一个门电路的输出不能直接或间接通过其他门电路回到同一门电路的输入端。如下图所示即为两种不允许的连接方式：

要求你设计的译码电路是一个有四个输入端和四个输出端的逻辑电路，该译码电路的输入和输出关系通过功能表给出，即给出每种输入组合下的四个输出端的情况。显然，一共有 $2^4=16$ 种输入组合。比如，一个由前述「与门」构成的 $2$ 输入，$2$ 输出的简单译码电路如下图所示（其中，A1, A2 是输入端，Y1, Y2 是输出端）

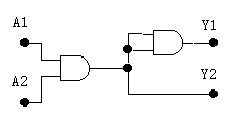
A1	A2	Y1	Y2
0	0	0
1
0	1
1		1

输入格式

第一行为一个正整数 $n(n\le 5)$，表示元件的种类数，其后有连续的 $n$ 行，每行描述一种元件。对正整数 $1\le k\le n$：

第 $k+1$ 行有四个以空格隔开的整数，依次为：$m_k,Y_{00},Y_{01},Y_{11}$。

其中，正整数 $m_k$ 表示第 $k$ 种元件的数目（$k$ 即这种元件的种类编号），所有元件的数目之和不会超过 $10$（用于实验的经费并不充足）。$Y_{ij}$ 表示两个输入端分别为 $i$ 和 $j$ 时的输出，即 $Y_{00},Y_{01},Y_{11}$ 是三个非 $0$ 即 $1$ 的数，分别表示在两个输入端均为 $0$；两个输入端一个为 $0$ 另一个为 $1$；以及两个输入端均为 $1$ 的时候，该元件的输出。

第 $n+2$ 到第 $n+17$ 行，表示需组成的集成电路的功能表，每行有 $8$ 个数，分别为 $0$ 或 $1$。其中，前四个数依次对应四个输入端（编号为 $1\sim 4$）的信号，不存在两行的前四个数完全相同；而后面四个数则对应在各输入端信号为前四个数时，四个输出端依次应输出的信号。

输出格式

第一行为一个单词，Yes 或 No，如果存在符合要求的设计方案，则为 Yes，否则为 No。

如果第一行是 No，则输出结束。

否则第二行只有一个非负整数 $p$，表示最少需要的门电路数目。下面 $p$ 行分别给出每个门电路在电路中的连接情况的描述。每行有四个以空格隔开的正整数：$S ,K, A, B$，其中 $S$ 表示该门电路的编号（所有用到的门电路按 $5\sim p+4$ 编号，$1\sim 4$ 的编号用来表示四个输入端）；$K$ 表示该元件的种类编号（按照输入文件中的顺序由 $1\sim n$ 编号）；$A$ 和 $B$ 分别表示接入该元件的两个输入端的门电路或译码电路输入端的编号（其中，$A<S,B<S$）。

最后一行有四个正整数，表示组成的译码电路的四个输出端分别所接的元件的编号（在 $1\sim p+4$ 之间）。

1
5 0 1 0
0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0
0 1 0 0 1 1 0 0
1 1 0 0 0 1 0 0
0 0 1 0 0 1 1 0
1 0 1 0 1 1 1 0
0 1 1 0 1 0 1 0
1 1 1 0 0 0 1 0
0 0 0 1 0 0 1 1
1 0 0 1 1 0 1 1
0 1 0 1 1 1 1 1
1 1 0 1 0 1 1 1
0 0 1 1 0 1 0 1
1 0 1 1 1 1 0 1
0 1 1 1 1 0 0 1
1 1 1 1 0 0 0 1

Yes
3
5 1 2 1
6 1 3 2
7 1 4 3
5 6 7 4