loj#P2353. 「NOI2007」 货币兑换
「NOI2007」 货币兑换
题目描述
小 最近在一家金券交易所工作。该金券交易所只发行交易两种金券: 纪念券(以下简称 券)和 纪念券(以下简称 券)。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动,两种金券都有自己当时的价值,即每一单位金券当天可以兑换的人民币数目。我们记录第 天中 券和 券的价值分别为 和 (元/单位金券)。为了方便顾客,金券交易所提供了一种非常方便的交易方式:比例交易法。比例交易法分为两个方面:
- 卖出金券:顾客提供一个 内的实数 作为卖出比例,其意义为:将 的 券和 的 券以当时的价值兑换为人民币;
- 买入金券:顾客支付 元人民币,交易所将会兑换给用户总价值为 的金券,并且,满足提供给顾客的 券和 券的比例在第 天恰好为 ;例如,假定接下来 天内的 的变化分别为:

假定在第一天时,用户手中有 元人民币但是没有任何金券。用户可以执行以下的操作:
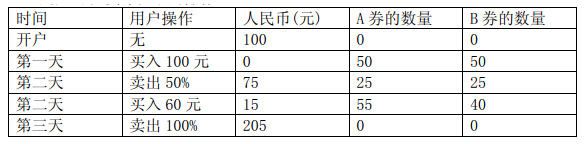
注意到,同一天内可以进行多次操作。小 是一个很有经济头脑的员工,通过较长时间的运作和行情测算,他已经知道了未来 天内的 券和 券的价值以及 。他还希望能够计算出来,如果开始时拥有 元钱,那么 天后最多能够获得多少元钱。
输入格式
输入第一行两个正整数 ,分别表示小 能预知的天数以及初始时拥有的钱数。
接下来 行,第 行三个实数 ,意义如题目中所述。
输出格式
只有一个实数 ,表示第 天的操作结束时能够获得的最大的金钱数目。答案与标准答案的绝对误差不超过 即视为答案正确。
3 100
1 1 1
1 2 2
2 2 3
225.000
数据范围与提示
数据范围
对于 的测试数据,满足 。
对于 的测试数据,满足 。
对于 的测试数据,满足 $ 1 \le N \le 10^5 , 0<A_K \le 10 , 0<B_K \le 10 , 0<\text{Rate}_K \le 100 , \text{MaxProfit} \le 10^9$ 。
提示
- 输入文件可能很大,请采用快速的读入方式。
- 必然存在一种最优的买卖方案满足:每次买进操作使用完所有的人民币;每次卖出操作卖出所有的金券。
