题目描述

译自 POI 2011 Round 2. Day 2. A「Tree Rotations」

园丁 Byteasar 正在种植一种叫 Rotatus Informatikus 的珍稀树种。它有一些有趣的特性：

• 树包含直的树枝，分叉和叶子。从地上长出来的树干也算树枝；
• 每根树枝要么以一个分叉点结束，要么以在顶端的一片叶子结束；
• 从一根树枝末端的分叉点恰好长出两根树枝——左树枝和右树枝；
• 树上每片叶子都用 $1\ldots n$ 范围内的整数编号。叶子编号两两不同；
• 通过一些园艺操作，在每个分叉点处可以进行一种叫「旋转」的操作，可以交换从这个分叉点长出的左右树枝。

树冠是从左到右读取叶子上的数而得到的序列。

Byteasar 是 Byteburg 人，就像所有真正的 Byteburg 人一样，他赞美整洁和秩序。他想知道进行一些旋转操作后，他的树会变得多整洁。树的整洁度用树冠的逆序对数表示。即序列 $a_1,a_2,\ldots ,a_n$ 中满足 $1\le i<j\le n,a_i\gt a_j$ 的数对 $(i,j)$ 的个数。

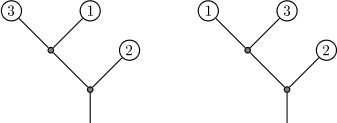
左边原树的树冠 $3,1,2$ 有两个逆序对。在一次旋转过后变成右边的数，树冠是 $1,3,2$，只有一个逆序对。这两棵树都有 $5$ 根树枝。

写一个程序，求出 Byteasar 的树经过旋转后树冠的最少逆序对数。

输入格式

第一行一个整数 $n$，表示表示 Byteasar 的树的叶子数。

接下来描述这棵树，这棵树利用递归定义：

• 如果在树干末端是一片标有 $p$ 的叶子（即，直接从地上长出来的树枝），那么对于这棵树的描述只包含一行一个整数 $p$；
• 如果在树干末端有分叉，那么这棵树的描述包含以下三部分：
  • 第一行包含一个整数 $0$；
  • 接下来是对左子树的描述（假设从分叉点分出的左树枝是左子树的树干）；
  • 最后是对右子树的描述（假设从分叉点分出的右树枝是右子树的树干）。

输出格式

一行一个整数，表示树冠的最少逆序对数。

3
0
0
3
1
2

1

数据范围与提示

对于全部数据，$1\le n\le 2\times 10^5,1\le p\le n$；

对于 $30\%$ 的分数，保证 $n\le 5\times 10^3$。

Task authors: Tomasz Kociumaka, Tomasz Walen.